Библиотека сайта rus-linux.net
Что каждый программист должен знать о памяти. Часть 5.
Оригинал: What every programmer should know about memory. Memory part 5: What programmers can do.
Автор: Ulrich Drepper
Дата публикации: 23.10.2007
Перевод: Капустин С.В.
Дата перевода: 30.10.2009
6. Что могут делать программисты - оптимизация кэша
6.2 Доступ к кэшу
Наиболее важные улучшения, которые программист может внести в работу с кэшами, относятся к кэшу уровня 1. Мы обсудим их первыми, до работы с другими уровнями. Очевидно, что оптимизация кэша уровня 1 повлияет и на другие кэши. Тема для любого доступа к памяти одна - улучшайте локальность (пространственную и временную) и выравнивайте код и данные.
6.2.1 Оптимизация доступа к кэшу данных 1 уровня
В разделе 3.3 мы уже видели насколько эффективное использование кэша L1d может повысить производительность. В этом разделе мы покажем, какие изменения в коде могут помочь её улучшить. В продолжение предыдушего раздела, мы сначала сконцентрируемся на оптимизации, которая позволит сделать доступ к памяти последовательным. Числа в разделе 3.3 показывают, что процессор автоматически делает предварительную выборку данных при последовательном доступе к памяти.
Для примера используется код перемножения матриц. Мы используем две квадратные матрицы размера 1000×1000. Для тех, кто забыл математику, произведение двух матриц A и B с элементами aij и bij, где 0 ≤ i,j < N, это матрица с элементами
Прямое использование этой формулы в программе на C может выглядеть так:
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
for (k = 0; k < N; ++k)
res[i][j] += mul1[i][k] * mul2[k][j];
Две исходные матрицы это mul1 и mul2. Матрица результата res изначально инициализирована нулями. Милая и простая реализация. Но должно быть очевидным, что мы имеем в точности ту же проблему, как на рисунке 6.1. Доступ к mul1 последовательный, а для mul2 внутренний цикл увеличивает номер строки. Это означает, что работа с mul1 идет как с левой матрицей на рисунке 6.1, а работа с mul2 идет как с правой матрицей. Это нехорошо.
Есть возможное решение, которое легко попробовать. Так как каждый элемент матрицы используется много раз, может стоит преобразовать ("транспонировать", говоря математическим языком) вторую матрицу mul2, перед тем как использовать её.
После транспозиции (традиционно обозначаемой верхним индексом ‘T’) мы обходим обе матрицы последовательно. В коде C это будет выглядеть так:
double tmp[N][N];
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
tmp[i][j] = mul2[j][i];
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
for (k = 0; k < N; ++k)
res[i][j] += mul1[i][k] * tmp[j][k];
Мы создаем временную переменную, которая будет содержать транспонированную матрицу. Это потребует выделения большего количества памяти, но затраты, можно надеяться, окупятся, так как 1000 не последовательных обращений на колонку обойдутся дороже (по крайней мере на современном оборудовании). Пора сделать какой-нибудь тест производительности. Результат на Intel Core 2 с тактовой частотой 2666МГц (в циклах процессора):
Исходная Транспонированная Циклы 16,765,297,870 3,922,373,010 Относительно 100% 23.4%
Простая трансформация матрицы дает выигрыш в 76.7%! Операция копирования более чем окупилась. 1000 не последовательных обращений к памяти - действительно проблема.
Следующий вопрос - наилучшее ли это решение? Мы определенно нуждаемся в альтернативном методе, который не требует дополнительного копирования. Не всегда можно позволить себе такую роскошь как копирование - матрица может быть слишком большой или доступная память слишком маленькой.
Поиск альтернативного метода нужно начать с пристального изучения используемой математики и операций, выполняемых в исходном решении. Тривиальные математические правила говорят, что порядок, в котором происходит суммирование для каждого элемента матрицы результата, не имеет значения, каждое слагаемое появляется только раз (мы игнорируем здесь арифметические эффекты, которые могут вызвать появление переполнения, потери значимости, округления). Это понимание позволяет нам искать решения, связанные с переупорядочиванием сложения, выполняемого во внутреннем цикле исходного кода.
Давайте посмотрим, в чем состоит проблема при исполнении исходного кода. Порядок, с которым происходит обращение к элементам mul2 такой: (0,0), (1,0), …, (N-1,0), (0,1), (1,1), …. Элементы (0,0) и (1,0) находятся в одной строке кэша, но пока внутренний цикл будет пройден один раз, эта строка давно уже будет исключена из кэша. Для этого примера каждый проход внутреннего цикла требует для каждой из трех матриц 1000 строк кэша (размером 64 байта для процессора Core 2). Это гораздо больше, чем 32Кб кэша L1d.
Но что, если мы будем обрабатывать две итерации среднего цикла вместе при прохождении внутреннего цикла? В этом случае мы используем два значения double из строки кэша, которые гарантированно будут в L1d. Мы сократим показатель промахов в L1d наполовину. Это определенно улучшение, но, в зависимости от размера строки кэша, это все еще может быть не наилучшим решением. Процессор Core 2 имеер размер строки кэша L1d 64 байта. Это значение можно выяснить используя
sysconf (_SC_LEVEL1_DCACHE_LINESIZE)
во время выполнения, или используя getconf в командной строке, так что программу можно скомпилировать для специфического размера строки кэша. При sizeof(double) равном 8 это означает, что для того, чтобы полностью использовать строку кэша, мы должны делать 8 итераций среднего цикла за один раз. Продолжая эту мысль, чтобы эффективно использовать также и матрицу res, т.е. чтобы записывать 8 результатов одновременно, мы должны делать также и 8 итераций внешнего цикла за один раз. Мы предполагаем здесь размер строки кэша 64, но код будет работать так же хорошо на системах с 32-байтными строками кэша, так как обе строки кэша будут использованы на 100%. В общем случае лучше всего зафиксировать размер строки кэша во время компиляции, используя утилиту getconf:
gcc -DCLS=$(getconf LEVEL1_DCACHE_LINESIZE) ...
Если бинарник предполагается к распространению, то нужно использовать наибольший размер строки кэша. Для очень маленького L1d это может означать, что не все данные попадут в кэш, но такие процессоры все равно не подходят для высокопроизводительных программ. Код, к которому мы приходим, должен выглядеть примерно так:
#define SM (CLS / sizeof (double))
for (i = 0; i < N; i += SM)
for (j = 0; j < N; j += SM)
for (k = 0; k < N; k += SM)
for (i2 = 0, rres = &res[i][j],
rmul1 = &mul1[i][k]; i2 < SM;
++i2, rres += N, rmul1 += N)
for (k2 = 0, rmul2 = &mul2[k][j];
k2 < SM; ++k2, rmul2 += N)
for (j2 = 0; j2 < SM; ++j2)
rres[j2] += rmul1[k2] * rmul2[j2];
Выглядит устрашающе. Это потому, что код содержит некоторые трюки. Самое заметное изменение состоит в том, что мы имеем 6 вложенных циклов. Внешние циклы имеют приращение SM (размер строки кэша, деленный на sizeof(double)). Это разделяет умножение на несколько более мелких задач, которые могут быть решены с большей локальностью кэша. Внутренние циклы выполняют итерации для индексов, пропущенных во внешних циклах. Получается снова три цикла. Единственный трюк здесь в том, что циклы для k2 и j2 идут в другом порядке. Это сделано потому, что при вычислении только одно выражение зависит от k2, а от j2 зависят два.
Остальные сложности являются результатом того, что компилятор gcc недостаточно умен, когда речь
идет об оптимизации индексов массива. Введение дополнительных переменных rres,
rmul1 и rmul2 оптимизирует код, вытягивая обычные выражения из внутренних
циклов настолько далеко, насколько это возможно. Правила по умолчанию для псевдонимов в языках C
и C++ не могут помочь компилятору сделать эти решения (если не используется ключевое слово
restrict, то любой доступ через указатели является потенциальным источником появления
псевдонимов). Вот почему Fortran все еще является предпочтительным языком для численного
программирования - он позволяет легче писать быстрый код. {В теории, ключевое слово
restrict, введенное в язык С в ревизии 1999 года, должно решить эту проблему. Компиляторы, однако, пока этого не поддерживают. Причина, в основном, в том, что существует очень много некорректного кода, который бы ввел компилятор в заблуждение и заставил его генерировать некорректный объектный код.}
В таблице 6.2 мы видим как вся эта работа окупается.
| Исходная | Транспонированная | Подматрицы | Векторизированно | |
|---|---|---|---|---|
| Циклы | 16,765,297,870 | 3,922,373,010 | 2,895,041,480 | 1,588,711,750 |
| Относительно | 100% | 23.4% | 17.3% | 9.47% |
Таблица 6.2: Замеры времени умножения матриц
Исключая копирование, мы получаем еще 6.1% производительности. Плюс нам не нужна дополнительная память. Входящие матрицы могут быть сколько угодно большими, пока матрица результата помещается в памяти. Это требование общего решения, которого мы теперь достигли.
В таблице 6.2 есть одна колонка, которую мы еще не объяснили. Большинство современных процессоров имеют сегодня поддержку векторизации. Часто подаваемые как мультимедийные расширения, эти специальные инструкции позволяют обрабатывать 2,4,8 или более значений одновременно. Часто это операции SIMD (Single Instruction, Multiple Data - одна инструкция много данных), дополненные другими, для приведения данных в нужную форму. Инструкции SSE2, которые поддерживают процессоры Intel, могут обрабатывать два двойных слова за одну операцию. Справочное руководство содержит список встроенных функций компилятора, которые предоставляют доступ к этим инструкциям SSE2. Если используются эти функции, программа работает еще на 7.3% быстрее, по сравнению с оригиналом. В результате мы получаем программу, которая делает работу за 10% времени работы исходного кода. Переведя в цифры, понятные для людей мы перешли от 318 мегафлоп к 3.35 гигафлоп. Так как мы интересуемся здесь только эффектами в памяти, код программы помещен в раздел 9.1.
Следует отметить, что в последней версии кода мы все еще имеем проблемы кэширования mul2 - предварительная загрузка так и не работает. Это нельзя решить без транспонирования матрицы. Может быть модули предварительной загрузки кэша станут умнее и смогут узнавать такую ситуацию, тогда дополнительных изменений не потребуется. 3.19 гигафлоп на процессоре 2.66ГГц с одноядерным кодом все равно неплохо.
В этом примере с произведением матриц мы оптимизировали использование загруженных строк кэша. Все байты строки кэша всегда используются. Мы просто делаем так, что они используются до того, как строка кэша исключена. Это определенно частный случай.
Более распространена ситуация, когда мы имеем структуры данных, которые заполняют одну или более строк кэша, хотя программа испольует всего несколько членов такой структуры данных за раз. На рисунке 3.11 мы уже видели эффекты большого размера структуры, у которой используется только несколько членов.
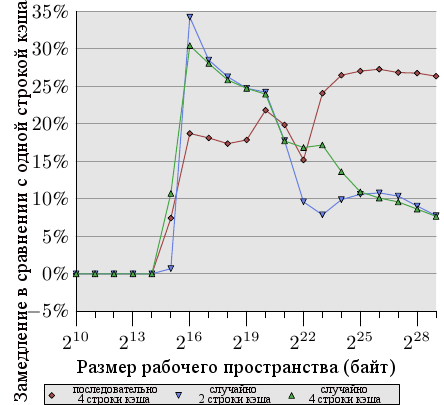
Рисунок 6.2: Распостранение на несколько строк кэша
Рисунок 6.2 показывает результаты еще одного набора тестов, использующих хорошо теперь известную программу. На этот раз складываются два значения из одного элемента списка. В одном случае оба элемента находятся в одной строке кэша, в другом случае один элемент в первой строке кэша элемента списка, а второй элемент - в последней строке кэша. График показывает замедление, которое мы имеем.
Неудивительно, что во всех случаях нет отрицательных эффектов, если рабочее пространство помещается в L1d. Когда L1d больше не хватает, приходится платить использованием двух строк кэша вместо одной. Красная линия показывает данные, когда список лежит последовательно в памяти. Мы видим две обычные ступени: около 17% ухудшения, пока достаточно кэша L2, и 27% - когда нужно использовать основную память.
В случае произвольного доступа данные выглядят немного по-другому. Ухудшение при рабочем пространстве, которое помещается в L2, находится между 25% и 35%. Потом оно уменьшается до примерно 10%. Это не из-за того, что издержки уменьшаются, наоборот, реальный доступ к памяти становится непропорционально более дорогим. Данные также показывают, что в некоторых случаях расстояние между элементами имеет значение. Кривая "случайные 4 строки кэша" показывает большие издержки, так как используются первая и четвертая строки кэша.
Легкий способ увидеть расположение структуры данных в строках кэша - это использовать программу pahole (см. [1]). Эта программа исследует структуры данных, определенные в бинарнике. Возьмем программу, содержащую такое определение:
struct foo {
int a;
long fill[7];
int b;
};
При компиляции на 64-битной машине вывод pahole содержит (кроме всего прочего) информацию, показанную на рисунке 6.3.
struct foo { int a; /* 0 4 */ /* XXX 4 bytes hole, try to pack */ long int fill[7]; /* 8 56 */ /* --- cacheline 1 boundary (64 bytes) --- */ int b; /* 64 4 */ }; /* size: 72, cachelines: 2 */ /* sum members: 64, holes: 1, sum holes: 4 */ /* padding: 4 */ /* last cacheline: 8 bytes */Рисунок 6.3: Вывод pahole Run
Этот вывод говорит о многом. Во-первых, он показывает, что структура данных использует более одной строки кэша. Программа подразумевает размер строки кэша текущего процессора, но это значение можно изменить, используя параметры командной строки. В случаях, когда размер структуры немного превосходит размер строки кэша и в памяти распределяется много объектов этого типа, особенно имеет смысл поискать пути к сжатию такой структуры. Может быть некоторые элементы могут иметь тип меньшего размера, или может быть некоторые поля в действительности являются флагами, которые могут быть реализованы, используя отдельные биты.
В случае нашего примера сжатие получить легко, оно предлагается самой программой. Вывод показывает, что есть дыра в четыре байта после первого элемента. Дыра вызвана требованиями выравнивания структуры и элемента fill. Легко видеть, что элемент b, который имеет размер четыре байта (об этом говорит 4 в конце строки), идеально подходит к этому промежутку. Результатом в этом случае является то, что промежутка больше не существует и структура данных помещается в одну строку кэша. Программа pahole может делать такую оптимизацию сама. Если использовать параметр —reorganize и добавить имя структуры в конце командной строки, выводом программы будет структура, оптимизированная по использованию строк кэша. Кроме перемещения элементов для заполнения промежутков, программа может оптимизировать битовые поля и комбинировать незначащие биты и дыры. Детали смотри в [1].
Иметь промежуток, достаточно большой для последующего элемента, - это, конечно, идеальная ситуация. Чтобы эта оптимизация была полезной, необходимо чтобы сам объект был выравнен по строке кэша. Остановимся на этом поподробнее.
Вывод pahole также позволяет легче определить, должны ли элементы быть переупорядочены так, чтобы элементы, которые вместе используются, вместе бы и хранились. Используя pahole, легко понять, какие элементы находятся в одной строке кэша и когда наоборот нужно переставить их, чтобы добиться этого. Это не автоматический процесс, но программа может сильно помочь.
- Всегда передвигать элемент структуры, который вероятнее всего будет критическим словом, в начало структуры.
- При обращении к структуре данных, когда порядок обращения не диктуется ситуацией, обращаться к элементам в том порядке, в котором они определены в структуре.
Для маленьких структур это означает, что программист должен располагать элементы в порядке, в котором они скорее всего будут использоваться. Это должно быть проделано гибко, с учетом других оптимизаций, таких как заполнение промежутков. Для более больших структур данных, эти правила должны применяться к каждому блоку размером в строку кэша.
Однако переупорядочивание элементов не стоит потраченного на него времени, если сам объект не выравнен. Выравнивание объекта определяется требованиями выравнивания типа данных. Каждый фундаментальный тип данных имеет свои требования выравнивания. Для структурных типов, наибольшие требования выравнивания из всех его элементов определяют выравнивание структуры. Это почти всегда меньше, чем размер строки кэша. Это означает, что даже если члены структуры выстроены так, чтобы попадать в одну строку кэша, сам размещенный объект может иметь выравнивание не подходящее к размеру строки кэша. Есть два пути проверить, что объект имеет выравнивание, которое использовалось при создании размещения структуры:
- объект может быть размещен в памяти с явным требованием выравнивания. При динамическом размещении вызов
mallocразместит объект с выравниванием совпадающим с выравниванием наиболее требовательного стандартного типа (обычноlong double). Однако можно использоватьposix_memalign, чтобы потребовать большего размера выравнивания.#include <stdlib.h> int posix_memalign(void **memptr, size_t align, size_t size);Эта функция сохраняет указатель на только что выделенную память в переменной
memptr. Блок памяти имеет размерsizeбайтов и выравнен по границе вalignбайтов.Для объектов, распределяемых компилятором (в
.data,.bss, и т.д., в стеке) можно использовать переменную attribute:struct strtype variable __attribute((aligned(64)));В этом случае
variableвыравнена по границе в 64 байт независимо от требования выравнивания структурыstrtype. Это работает и для глобальных, и для автоматических переменных.Однако это не работает для массивов. Только первый элемент массива будет выравнен, если размер каждого элемента массива не кратен размеру выравнивания. Это также означает, что каждая единичная переменная должна быть соответственно объявлена. Использование
posix_memalignтакже не является полностью бесплатным, так как требования выравнивания обычно ведут к фрагментации и/или более высокому потреблению памяти. - требование выравнивания типа может быть изменено, используя атрибут типа:
struct strtype { ...members... } __attribute((aligned(64)));Это заставит компилятор выделять все объекты с подходящим выравниванием, включая массивы. Однако программист должен позаботиться о запросе подходящего выравнивания для динамически размещаемых объектов. Следовательно, нужно снова использовать
posix_memalign. Удобно использовать операторalignofиз gcc и передавать значение второго параметраposix_memalign.
Ранее упомянутые в этом разделе мультимедийные расширения почти всегда требуют, чтобы доступ к памяти был выравнен. То есть, для чтения из памяти по 16 байт, адрес предполагается выравненным по 16 байт. Процессоры x86 и x86-64 имеют специальные варианты операций с памятью, которые могут осуществлять невыравненный доступ, но они медленнее. Это жесткое требование выравнивания не является новым для большинства RISC архитектур, которые требуют полного выравнивания для любого доступа к памяти. Даже если архитектура поддерживает невыравненный доступ, он иногда медленнее, чем использование соответствующего выравнивания, особенно если невыравненное чтение или запись должны использовать две строки кэша вместо одной.
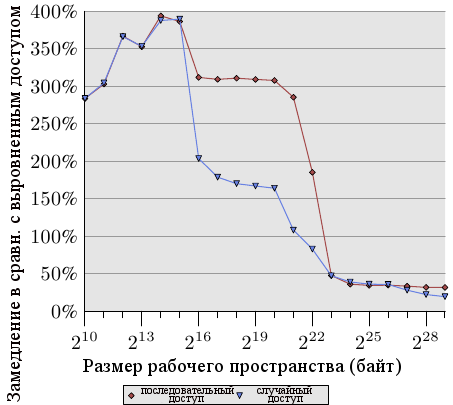
Рисунок 6.4: Отставание невыравненного доступа
Рисунок 6.4 показывает эффекты невыравненного доступа к памяти. Описанный выше тест измеряет время обращения к элементам данных (последовательным или произвольным в памяти), причем один раз список элементов выравнен в памяти, а один раз выравнивание намеренно нарушено. График показывает замедление программы, вызванное невыравненным доступом. Эффект более значительный для случая последовательного доступа по сравнению со случайным доступом потому что в последнем случае затраты на невыравненный доступ частично скрыты более высокими общими затратами на доступ к памяти. В случае последовательного доступа, для размеров рабочего пространства, умещающихся в кэш L2, замедление порядка 300%. Это может быть объяснено снижением эффективности кэша L1. Некоторые операции приращения теперь затрагивают две строки кэша, и обращение к элементу списка теперь требует чтения двух строк кэша. Соединение между L1 и L2 просто слишком перегружено.
Для очень больших размеров рабочего пространства эффект невыравненного доступа составляет от 20% до 30%, что все еще много, учитывая что выравненный доступ для таких размеров долог. Этот график должен показать, что к выравниванию нужно подходить серьезно. Даже если архитектура поддерживает невыравненный доступ, к нему не нужно относится так, как если бы он был так же хорош, как выравненный.
Однако, есть некоторые отступления от этих требований выравнивания. Если автоматическая переменная имеет требование выравнивания, то компилятор должен проследить, чтобы это происходило во всех случаях. Это нетривиальная задача, так как компилятор не имеет контроля над местами вызова и тем, как они обращаются со стеком. Эта проблема может быть решена двумя путями:
- Сгенерированный код активно выравнивает стек, вставляя промежутки при необходимости. Это требует от кода проверки на выравнивание, создания выравнивания и, позднее, отмены выравнивания.
- Требовать, чтобы все вызовы выравнивали стек.
Все обычно используемые двоичные интерфейсы приложений (ABI - application binary interface) идут вторым путем. Программы скорее всего дадут сбой, если вызов нарушает правило и вызываемое требует выравнивания. Однако поддержка выравнивания не дается бесплатно.
Размер стека функции не обязательно кратен размеру, по которому идет выравнивание. Это означает, что необходимо заполнение, если другие функции вызываются из этого стека. Другое дело, что размер стека в большинстве случаев известен компилятору и, следовательно, он знает как подстроить указатель стека, чтобы любая функция, вызываемая из стека была выравнена. На самом деле, большинство компиляторов просто округляют размер стека, чтобы сделать это.
Это простое решение невозможно, если используются массивы переменной длины или alloca. В этом случае общий размер стека известен только во время выполнения. В таком случае, возможно, понадобится активный контроль за выравниванием, что сделает сгенерированный код (немного) медленнее.
На некоторых архитектурах только мультимедийные расширения требуют выравнивания, стеки на таких архитектурах всегда минимально выравнены для обычных типов данных, обычно по 4 или 8 байт для 32- и 64-битовых архитектур соответственно. На таких системах принудительное выравнивание приносит ненужные затраты. Это означает, что в этом случае мы можем захотеть избавиться от строгих требований выравнивания, если мы знаем что от него ничего не зависит. Замыкающие функции (которые не вызывают другие функции), не исполняющие мультимедийных операций, не нуждаются в выравнивании. Также как и функции, которые вызывают только функции, не нуждающиеся в выравнивании. Если может быть идентифицирован достаточно большой набор функций, программа может захотеть ослабить требование выравнивания. Для бинарников x86 gcc имеет поддержку для ослабленных требований выравнивания стека:
-mpreferred-stack-boundary=2
Если в этой опции задано значение N, то требование выравнивания для стека будет задано как 2N байт. Так, если исползуется значение 2, то требование выравнивания для стека будет снижено со значения по умолчанию (которое равно 16 байт) до всего 4 байт. В большинстве случаев это означает, что не нужно никаких дополнительных операций выравнивания, так как обычные операции кэша push и pop и так работают по четырехбайтным границам. Эта машиннозависимая опция может помочь уменьшить размер кода и улучшить скорость выполнения. Но её невозможно применять на множестве других архитектур. Даже на x86-64 это в общем неприменимо, так как x86-64 ABI требует, чтобы параметры с плавающей точкой передавались в регистр SSE, а инструкции SSE требуют полного 16-байтного выравнивания. Тем не менее, когда эта опция применима, она может оказать заметное влияние.
Эффективное размещение элементов структуры и выравнивание - не единственные аспекты структур данных, которые влияют на эффективность кэша. Если используется массив структур, все определения структур влияют на производительность. Вспомните результаты на рисунке 3.11: в этом случае мы имели увеличивающийся размер неиспользуемых данных в элементах массива. Результатом было то, что предварительная выборка была все менее эффективной и программа, для больших объемов данных, стала менее эффективной.
Для больших размеров рабочего пространства важно использовать доступный кэш так хорошо, как это возможно. Чтобы добиться этого, возможно, будет необходимо преобразовать структуру данных. Хотя для программиста удобнее хранить все данные, которые концептуально объединены вместе, в одной структуре данных, это может оказаться не лучшим подходом с точки зрения производительности. Предположим, что у нас есть следующая структура данных:
struct order {
double price;
bool paid;
const char *buyer[5];
long buyer_id;
};
Далее, предположим, что эти записи хранятся в большом массиве и часто запускаемая процедура добавляет ожидаемые платежи по выставленные счетам. При таком сценарии, память, используемая для полей buyer и buyer_id, без необходимости загружается в кэш. Судя по данным рисунка 3.11, программа будет работать в 5 раз хуже, чем она могла бы.
Намного лучше разделить структуру данных order на две структуры, в первой используя первые два поля, остальные поля где-то еще. Это изменение определенно усложнит программу, но выигрыш в производительности может оправдать затраты.
И наконец, давайте рассмотрим еще одну оптимизацию использования кэша, которая, хотя и применима к другим кэшам, в первую очередь чувствуется при доступе к L1d. Как видно из рисунка 3.8, возрастающая ассоциативность кэша улучшает обычные операции. Чем больше кэш, тем обычно выше ассоциативность. Кэш L1d слишком велик, чтобы быть полностью ассоциативным, но не настолько велик, чтобы иметь такую же ассоциативность как L2. Это может быть проблемой, если много объектов рабочего пространства попадают в один и тот же набор кэша. Если это приводит к исключению из кэша из-за перегруженности набора, программа может испытывать задержки, даже если большая часть кэша свободна. Эти промахи кэша иногда называют конфликтные промахи. Так как адресация L1d использует виртуальные адреса, это то, над чем программист может иметь контроль. Если переменные, которые вместе используются, хранятся тоже вместе, то вероятность того, что они попадут в один набор минимальна. Рисунок 6.5 показывает как быстро проблема может появиться.
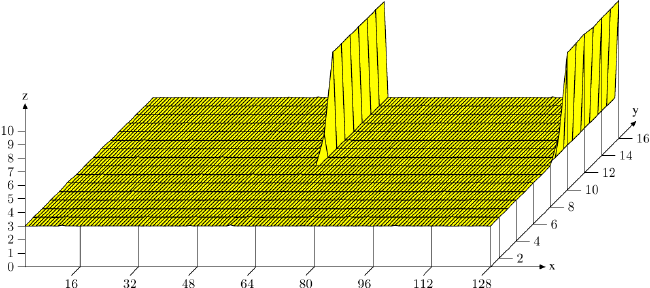
Рисунок 6.5: Эффекты ассоциативности кэша
На рисунке - знакомый теперь тест Follow с NPAD=15 {тест производился на 32-битной машине, следовательно
NPAD=15 означает одну 64-байтную строку кэша на один элемент списка.}, измеренный специальным образом. На оси X - расстояние между двумя элементами списка, измеренное пустыми элементами списка. Другими словами, расстояние в 2 означает, что адрес следующего элемента находится через 128 байт от предыдущего. Все элементы размещены в виртуальном адресном пространстве на одном расстоянии друг от друга. Ось Y показывает общую длину списка. Используется только 16 элементов, что означает, что общее рабочее пространства будет составлять от 64 до 1024 байт. Ось Z показывает среднее количество циклов, необходимое для обхода каждого элемента списка.
Результат, показанный на рисунке, не должен вызвать удивления. Если используется мало элементов, то все они помещаются в L1d и время доступа составляет только 3 цикла на элемент списка. То же верно для почти всех размещений элементов списка: виртуальное адресное пространство отлично отображается в слоты L1d, почти без конфликтов. Есть два (на этом графике) особых значения расстояния, для которых ситуация другая. Если расстояние кратно 4096 байтам (т.е. дистанции в 64 элемента) и длина списка больше, чем восемь, то среднее количество циклов для доступа к элементу списка возрастает драматически. При такой ситуации все записи находятся в одном наборе и когда длина списка больше, чем ассоциативность, записи исключаются из L1d и должны быть заново считаны из L2 при следующем обходе. Результатом является 10 циклов на элемент списка.
Из этого графика мы можем определить, что процессор использует кэш L1d размером 32Кб и ассоциативностью 8. Это означает, что тест, при необходимости, может быть использован для определения этих значений. Те же эффекты могут быть измерены для кэша L2, но там ситуация сложнее, так как L2 использует физические адреса и он намного больше.
Для программистов это означает, что ассоциативность - это то, на что стоит обращать внимание. Размещать данные на границах, являющихся степенью двойки, в реальной жизни приходится достаточно часто, а это как раз та ситуация, которая может легко привести к описанным выше эффектам и снижению производительности. Невыравненные доступы могут увеличить вероятность конфликтных промахов, так как каждый доступ может потребовать дополнительной строки кэша.

Рисунок 6.6: Адреса банков L1d у AMD
Если выполнена такая оптимизация, то возможна ещё одна похожая оптимизация. Процессоры AMD, по крайней мере, реализуют L1d как несколько индивидуальных банков. L1d может получать два слова за цикл, но только если оба слова хранятся в разных банках, или в банке с одинаковым индексом. Адрес банка закодирован в младших битах виртуального адреса, как показано на рисунке 6.6. Если переменные, которые используются вместе, сохраняются также вместе, высока вероятность того, что они в разных банках, или в одном банке с одинаковым индексом.
[1] Melo, Arnaldo Carvalho de. The 7 dwarves: debugging information beyond gdb. Proceedings of the linux symposium. 2007.
[2] Drepper, Ulrich. Futexes Are Tricky., 2005. http://people.redhat.com/drepper/futex.pdf.
[3] Huggahalli, Ram, Ravi Iyer and Scott Tetrick. Direct Cache Access for High Bandwidth Network I/O. , 2005.
| Назад | Оглавление | Вперед |

![[formula]](/MyLDP/hard/memory/5/matrixmult.png)
![[formula]](/MyLDP/hard/memory/5/matrixmultT.png)