Библиотека сайта rus-linux.net
Краткое руководство по статистическим моделям и построению графиков в GNU R
Оригинал: A quick GNU R tutorial to statistical models and graphics
Автор: Renata Rendek
Дата публикации: февраль 2013 года
Перевод: А. Кривошей
Дата перевода: май 2013 г.
Предыдущие части: Введение в GNU R, Запуск GNU R в Linux, Введение в базовые операции, функции и структуры данных GNU R.
1. Введение
В данном кратком руководстве по статистическим моделям и графическим возможностям GNU R мы рассмотрим пример простой линейной регрессии и узнаем о том, как выполнять базовый статистический анализ данных. Наш пример мы будем иллюстрировать графически. что позволит нам ближе познакомиться с построением графиков и диаграмм в GNU R.
2. Модели и формулы в R
Под моделью в статистике мы понимаем краткое описание данных. Такое представление данных, как правило, описывается математической зависимостью. В R есть свой собственный способ представления зависимостей между переменными. Например зависимость y=c0+c1x1+c2x2+...+cnxn+r в R записывается как:
y~x1+x2+...+xn,
Это объект формула.
3. Пример линейной регрессии
Теперь рассмотрим пример линейной регрессии в GNU R, состоящий из двух частей. В первой части мы изучим зависимость между значениями финансового индекса, выраженными в американских долларах, и теми же значениями, выраженными в канадских долларах. Далее, во второй части примера, мы добавим в наш анализ еще одну переменную, выражающую значения индекса в евро.
3.1. Простая линейная регрессия
Скачайте файл с данными примера в свою рабочую директорию: regression-example-gnu-r.csv
Запустите R:
$ R
и считайте данные из нашего файла:
> returns<-read.csv("regression-example-gnu-r.csv",header=TRUE)
Вы можете просмотреть имена переменных с помощью команды:
>names(returns) [1] "USA" "CANADA" "GERMANY"
Теперь необходимо определить нашу статистическую модель и рассчитать линейную регрессию. Это можно сделать с помощью следующих нескольких строк кода:
> y<-returns[,1] > x1<-returns[,2] > returns.lm<-lm(formula=y~x1)
Чтобы вывести краткую информацию о регрессионном анализе, мы исполняем функцию summary() на возвращаемом объекте.
> summary(returns.lm)
Call:
lm(formula = y ~ x1)
Residuals:
Min 1Q Median 3Q Max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.174e-05 3.862e-05 0.822 0.411
x1 9.275e-01 4.880e-03 190.062 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.003921 on 10332 degrees of freedom
Multiple R-squared: 0.7776, Adjusted R-squared: 0.7776
F-statistic: 3.612e+04 on 1 and 10332 DF, p-value: < 2.2e-16
Эта функция выводит соответствующие результаты. Оценочные коэффициенты здесь c0~3.174e-05 и c1 ~9.275e-01. P-значения подтверждают, что оцениваемое пересечение c0 незначительно отличается от нуля, поэтому им можно пренебречь. Второй коэффициент значительно отличается от нуля, так как p-значение <2e-16. Поэтому наша модель представлена формулой y=0.93 x1. Далее, R2 = 0.78, что значит, что в 78% случаев изменения x приводят к изменению y. Другими словами, точность подбора уравнения регрессии составляет 78%.
3.2. Множественная линейная регрессия
Давайте добавим к нашей модели еще одну переменную и выполним множественный регрессионный анализ. Вопрос в том, приведет ли добавление переменной к повышению точности нашей модели.
> x2<-returns[,3]
> returns.lm<-lm(formula=y~x1+x2)
> summary(returns.lm)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.385e-05 3.035e-05 0.786 0.432
x1 6.736e-01 4.978e-03 135.307 <2e-16 ***
x2 3.026e-01 3.783e-03 80.001 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.003081 on 10331 degrees of freedom
Multiple R-squared: 0.8627, Adjusted R-squared: 0.8626
F-statistic: 3.245e+04 on 2 and 10331 DF, p-value: < 2.2e-16
Выше вы можете видеть результата множественного регрессионного анализа после добавления переменной x2. Эта переменная содержит значения финансового индекса в евро. Теперь мы получили более точную модель, так как скорректированное значение R2 достигло 0,86, что значительно больше полученного ранее 0,76. Обратите внимание, что мы сравнивали скорректированное значение R2, так как необходимо принимать во внимание количество переменных и размер выборки. Коэффициент пересечения снова незначителен, поэтому модель имеет вид y=0.67x1+0.30x2.
Обратите внимание, что мы можем ссылаться на наши векторы данных по их именам, например:
> lm(returns$USA~returns$CANADA)
Call:
lm(formula = returns$USA ~ returns$CANADA)
Coefficients:
(Intercept) returns$CANADA
3.174e-05 9.275e-01
4. Графика
В этом разделе мы продемонстрируем, как использовать R для визуализации данных. Мы изучим работу с функциями plot(), boxplot(), hist(), qqnorm().
4.1. Диаграммы рассеяния
Вероятно простейшим примером графиков, доступных в R, является диаграмма рассеяния. Мы используем его для того, чтобы проиллюстрировать зависимость между значениями финансового индекса, выраженными в американских и канадских долларах с помощью функции plot():
> plot(returns$USA, returns$CANADA)
В результате выполнения этой функции мы получим показанный ниже график:
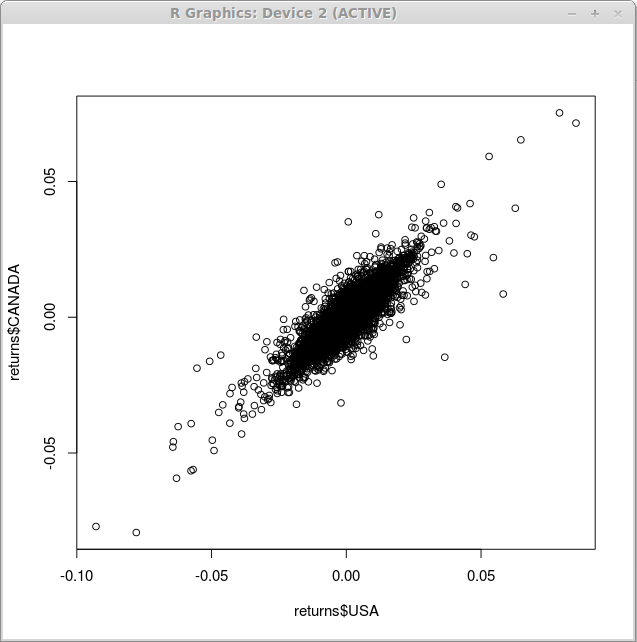
Один из самых важных аргументов, который используется с этой функцией - "type". Он определяет тип выводимого графика. Доступные типы:
type="p" - выводит отдельные точки (принято по умолчанию);
type="l" - рисует линии;
type="b"- выводит точки, соединенные линиями (вместе);
type="o"- рисует точки перекрытые линиями;
type="h" - рисует вертикальные линии от точек до нулевого уровня оси (график high-density);
type="s", type="S" - графическая ступенчатая функция. В первом варианте, верх вертикали определяет точу, а во втором - низ;
type="n" - не рисовать ничего. Однако оси по-прежнему выводятся (по умолчанию) и система координат создается в соответствии с данными. Идеально подходит для создания участков последовательностью низкоуровневых графических функций.
Для того, чтобы наложить на диаграмму рассеяния график регрессии, мы используем функцию curve() с аргументами "add" и "col", которые определяют, что линия должна быть добавлена к существующему графику, и цвет линии соответственно.
> curve(0.93*x,-0.1,0.1,add=TRUE,col=2)
Следовательно, наш график изменится следующим образом:
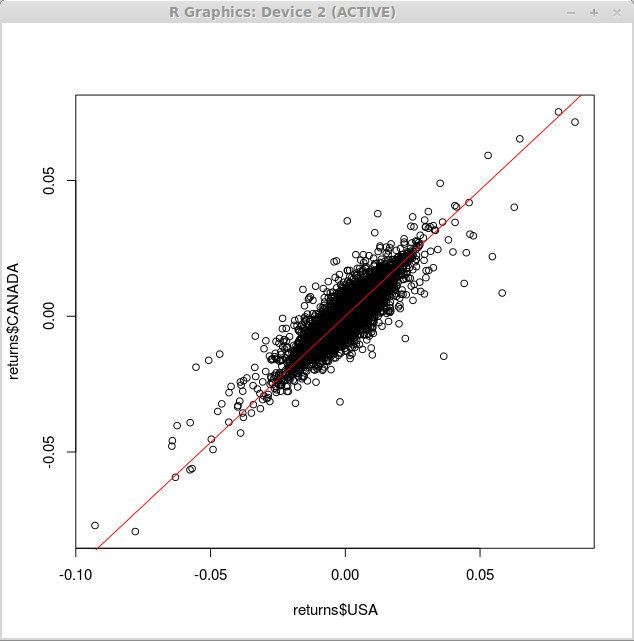
Более подробную информацию о функциях plot() или lines() можно получить с помощью функции help(), например:
>help(plot)
4.2. График "ящик с усами"
Теперь давайте посмотрим, как использовать функцию boxplot() для иллюстрации данных описательной статистики. Во-первых, рассчитаем описательные статистики для наших данных с помощью функции summary(), а затем применим к результату функцию boxplot():
> summary(returns)
USA CANADA GERMANY
Min. :-0.0928805 Min. :-0.0792810 Min. :-0.0901134
1st Qu.:-0.0036463 1st Qu.:-0.0038282 1st Qu.:-0.0046976
Median : 0.0005977 Median : 0.0005318 Median : 0.0005021
Mean : 0.0003897 Mean : 0.0003859 Mean : 0.0003499
3rd Qu.: 0.0046566 3rd Qu.: 0.0047591 3rd Qu.: 0.0056872
Max. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688
Обратите внимание, что описательные статистики для всех трех векторов похожи, поэтому мы можем ожидать, что графики для всех трех наборов финансовых данных также будут похожи. Далее, мы исполняем функцию boxplot():
> boxplot(returns)
В результате получаем следующие три графика.
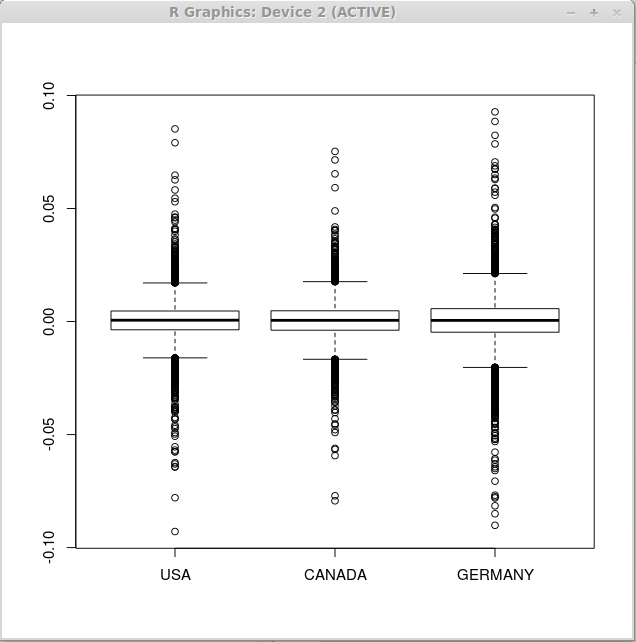
4.3. Гистограммы
В этом разделе мы рассмотрим гистограммы. Гистограмму частот вы уже могли видеть в одной из предыдущих статей. Теперь мы рассмотрим гистограмму распределения относительных частот для нормализованных значений и сравним ее с кривой нормального распределения.
Сначала нормализуем значения деноминированного в американских долларах индексах, чтобы получить нулевое среднее значение и дисперсию, равную единице, для того, чтобы иметь возможность сравнить реальные данные с теоретической функцией стандартного нормального распределения.
> retUS.norm<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA)) > mean(retUS.norm) [1] -1.053152e-17 > var(retUS.norm) [1] 1
Теперь мы построим гистограмму распределения для таких нормализованных значений и кривую нормального распределения поверх нашей гистограммы:
> hist(retUS.norm,breaks=50,freq=FALSE) > curve(dnorm(x),-10,10,add=TRUE,col=2)
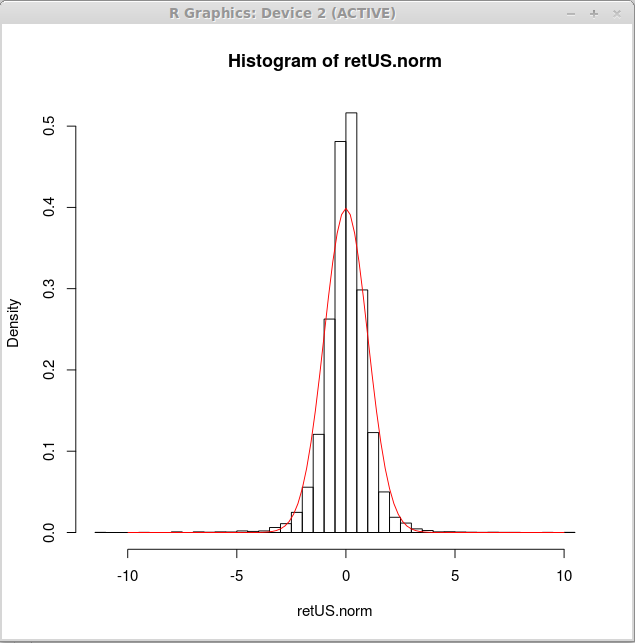
Визуально наши данные не соответствуют кривой нормального распределения, и для их корректного описания требуется другое распределение. Как его найти, мы узнаем в следующих статьях. Сейчас же мы можем отметить, что такое распределение должно иметь более острый главный пик и большие хвосты.
4.4. График квантиль-квантиль
Еще один полезный инструмент статистического анализа - график квантиль-квантиль, который позволяет сравнить квантили эмпирического и теоретического распределений. Если они хорошо совпадают, вы должны увидеть прямую линию. Давайте сравним распределение погрешностей нашего регрессионного анализа. Сначала мы построим график квантиль-квантиль график для простой линейной регрессии, а затем для множественной. Мы будем использовать график квантиль-квантиль нормального типа. Это значит, что теоретические квантили графика соответствуют квантилям нормального распределения.
Первый график соответствует погрешностям простой линейной регрессии, полученным с помощью функции qqnorm() следующим способом:
> returns.lm<-lm(returns$US~returns$CANADA) > qqnorm(returns.lm$residuals)
Соответствующий график показан ниже:
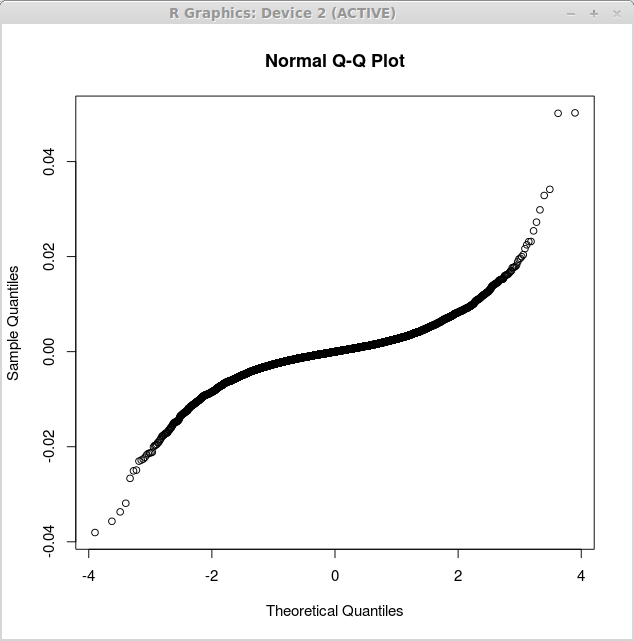
Обратите внимание, что второй график ближе к прямой линии. Это показывает, что погрешности множественной регрессии ближе к нормальному распределению, а значит вторая модель лучше соответствует реальным данным.
5. Заключение
В этой статье мы получили представление о статистическом моделировании в GNU R на примере линейной регрессии. Мы также обсудили некоторые часто используемые в статистике графики. Надеюсь, вы почерпнули здесь что-нибудь полезное для себя. В следующих статьях мы рассмотрим более сложные аспекты применения R для статистического анализа, а также для программирования.






