Библиотека matplotlib

Оригинал: matplotlib
Автор: John Hunter, Michael Droettboom, перевод: А.Панин

11.4. Преобразования

Каждый класс Artist имеет узел преобразования, содержащий данные о том, как произвести преобразование из одной системы координат в другую. Эти узлы преобразования объединены друг с другом в рамках ориентированного графа, в котором каждый узел зависит от родительского узла. По пути от ребер к корню графа, координаты пространства данных для любой вершины могут быть преобразованы в координаты результирующего файла. Большинство преобразований также является обратимым. Это обстоятельство позволяет выбрать элемент графика и получить его координаты пространства данных. Граф преобразований устанавливает зависимости между вершинами: при изменении данных преобразования для корня графа, таком, как изменение границ координатных осей в классе Axes, все данные преобразований, связанные с классом Axes становятся недействительными, так как точки должны быть перерисованы. Данные преобразований, связанные с другими классами Axes для рисунка, конечно же, не должны затрагиваться с целью предотвращения ненужных повторных расчетов и повышения интерактивности операций.

Узлы преобразований могут выполнять как простые афинные, так и неафинные преобразования. Афинные преобразования являются семейством преобразований, сохраняющих прямыми линии и соотношения расстояний изображения, выполняя его вращение, преобразование, масштабирование и наклон. Двумерные афинные преобразования представляются с помощью матрицы афинного преобразования размерностью 3x3. Координаты точки после преобразования (x',y') вычисляются путем умножения матрицы с начальными координатами (x, y) на следующую матрицу:

Координаты двумерного пространства могут быть просто преобразованы путем умножения их на матрицу трансформации. Афинные трансформации также обладают полезным свойством, заключающимся в том, что они могут быть объединены с помощью матричного умножения. Это значит, что для выполнения серий афинных преобразований матрицы трансформации могут быть перемножены только один раз, после чего результирующая матрица может быть использована для преобразования координат. Фреймворк преобразования координат библиотеки matplotlib автоматически объединяет (замораживает) матрицы афинных преобразований для сокращения объема вычислений. Возможность использования быстрых афинных преобразований важна, так как с помощью них можно повысить производительность интерактивного перемещения и масштабирования изображения в окне графического интерфейса приложения.

Не являющиеся афинными преобразования в рамках библиотеки matplotlib используют функции языка Python, поэтому они являются действительно произвольными. В рамках основного кода библиотеки matplotlib неафинные преобразования используются для логарифмического масштабирования, создания графиков в полярных координатах и создания географических проекций (Рисунок 11.5). Эти неафинные преобразования могут свободно смешиваться с афинными в графе преобразования. Библиотека matplotlib автоматически упростит афинные преобразования и перейдет к использованию произвольных функций только для части неафинных преобразований.

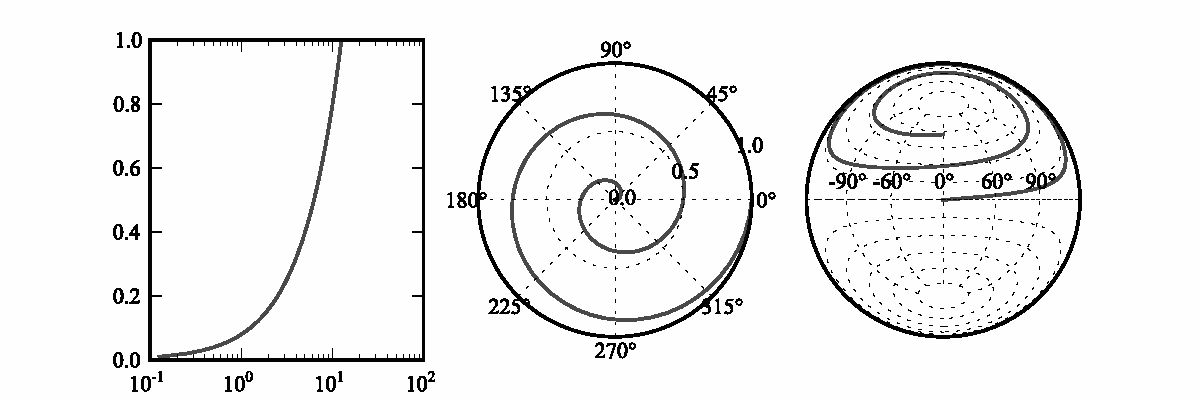
Рисунок 11.5: Одни и те же данные на графиках, подвергнутые трем неафинным преобразованиям: к логарифмическим координатам, к полярным координатам и к координатам проекции Ламберта

Используя эти простые операции, библиотека matplotlib может выполнять некоторые достаточно сложные задачи. Смешанное преобразование выполняется специальным узлом преобразования и предназначено для выполнения одного преобразования для оси x и другого преобразования для оси y. Это, конечно же, становится возможным только в случае, если рассматриваемые преобразования являются "разделяемыми", что подразумевает независимость координат x и y, ну а сами преобразования могут быть как афинными, так и неафинными. Эта возможность используется, например, для создания графиков в логарифмической системе координат, где одна или обе оси x и y могут использовать логарифмическую систему координат. Возможность использования смешанного преобразования позволяет совмещать доступные системы координат произвольным образом. Другой возможностью графа преобразования является разделение осей. Существует возможность "связать" ограничения одного графика с другим и быть уверенным в том, что при перемещении или масштабировании одного из графиков, состояние другого графика будет изменено соответствующим образом. В этом случае один и тот же узел преобразования просто совместно используется двумя осями, которые могут относиться даже к разным изображениям. На Рисунке 11.6 показан пример графа преобразования с задействованием некоторых из этих дополнительных возможностей. Ось axes1 является осью x в логарифмической системе координат; оси axis1 и axis2 совместно используют одну и ту же ось y.

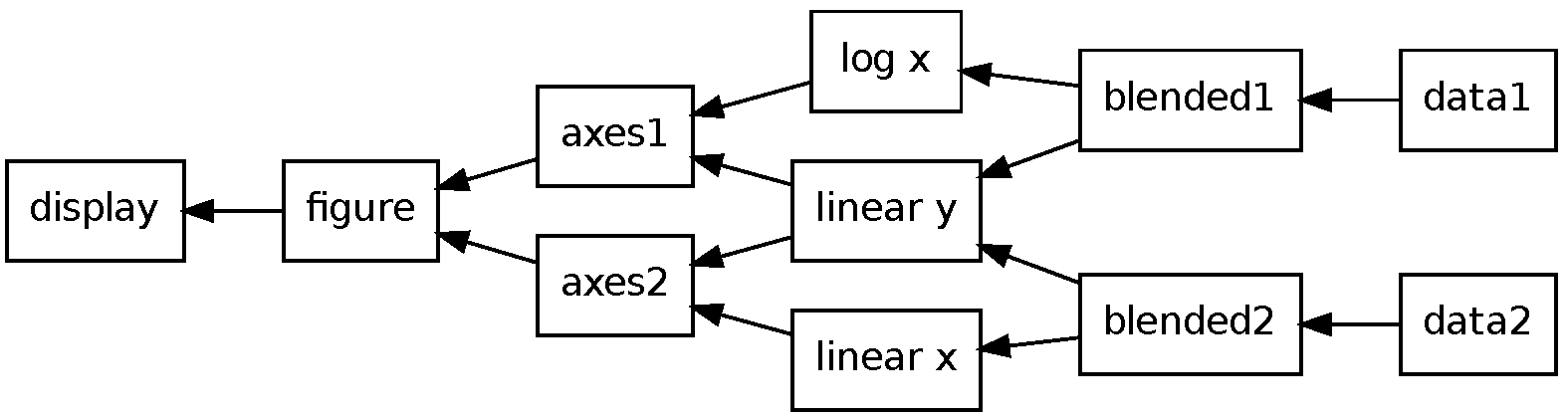
Рисунок 11.6: Пример графа преобразования

Далее: Процесс обработки полилиний