Библиотека matplotlib

При создании графика с помощью линий библиотека matplotlib выполняет ряд шагов для преобразования необработанных данных в линию на экране. В ранних версиях matplotlib эти шаги были взаимосвязаны. С тех пор код подвергся рефакторингу, поэтому они стали отдельными шагами процесса "преобразования путей". Это обстоятельство позволяет каждой системе вывода данных выбирать шаги процесса обработки для непосредственного выполнения, так как некоторые шаги полезны только в определенных контекстах.

• Преобразование: Координаты преобразуются из координат данных в координаты изображения. Если это преобразование является полностью афинным, как описано выше, этот процесс заключается в простом умножении матриц. Если требуются произвольные преобразования, вызываются функции для преобразования координат в пространство изображения.
• Обработка отсутствующих данных: Массив данных может содержать участки, данные из которых отсутствуют или являются некорректными. Пользователь может указать на это либо приравняв их значения к NaN, либо использовав маскированные массивы библиотеки numpy. Векторные форматы файлов, такие, как PDF и библиотеки вывода изображений, такие, как Agg обычно не используют концепцию отсутствующих данных при построении полилиний, поэтому данный шаг процесса должен пропускать сегменты отсутствующих данных с помощью команд MOVETO, которые указывают библиотеке вывода изображения на необходимость перемещения начальной точки перед продолжением рисования.
• Вырезка: Наличие точек вне границ изображения может привести к увеличению размера файла из-за включения множества невидимых точек. Еще более важно то, что очень большие или очень малые значения координат могут привести к ошибкам переполнения при создании выходного файла, которые в результате приведут к полностью испорченному выходному файлу. На этом шаге процесса осуществляется обрезка изображения на основе точек входа и выхода полилинии за границы изображения для преодоления всех этих проблем.
• Привязка к центру пикселей: идеально вертикальные и горизонтальные линии могут выглядеть размыто из-за сглаживания в том случае, если их центры не выровнены по центру пикселя (обратитесь к Рисунку 11.7). При выполнении шага привязки к центру пикселей в процессе обработки полилиний в первую очередь устанавливается, состоит ли полилиния только из горизонтальных и вертикальных сегментов (как в случае прямоугольника со сторонами, ориентированными по координатным осям), и, в случае установления этого факта, сдвигает каждую вершину результирующей полилинии к ближайшему центру пикселя. Этот шаг выполняется только для систем вывода данных в растровые форматы, так как векторные форматы должны продолжить использовать точные данные. Некоторые программы просмотра файлов векторных форматов, такие, как Adobe Acrobat, выполняют операции привязки к центру пикселей при просмотре на экране.
  
  Рисунок 11.7: Операция привязки к центру пикселей крупным планом: слева линия без привязки; справа - с привязкой.
• Упрощение: При построении действительно сложных графиков множество точек на линии может быть на самом деле невидимым. Это особенно актуально в случае отображения амплитуды шума аудиосигнала на графике. Включение этих точек в график увеличивает размер файла и даже может привести к достижению ограничения разрешенного количества точек для данного формата. Следовательно, любые точки, лежащие непосредственно на линии между двумя соседними точками, удаляются (обратитесь к Рисунку 11.8). Алгоритм определения использует пороговое значение, устанавливаемое на основе того, что будет видимо при заданном пользователем разрешении.
  
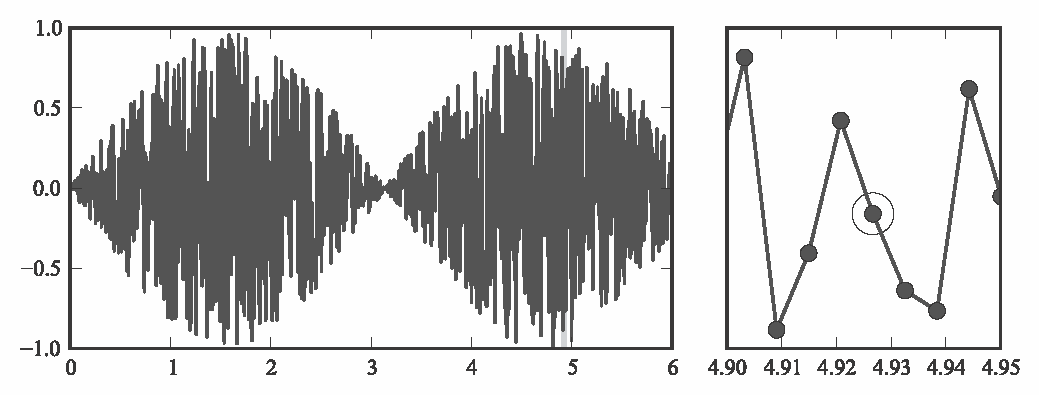
  Рисунок 11.8: Изображение справа является увеличенным фрагментом изображения слева. Обведенная вершина автоматически удаляется с помощью механизма упрощения, так как она лежит непосредственно на линии между соседними вершинами и, следовательно, является избыточной.