Библиотека сайта rus-linux.net
Создание фракталов в PDL
Сравнение производительности PDL, IDL, MATLAB, Octave, C и FORTRAN77 при создании фрактала
Оригинал: Generating cool fractals
Автор: Xavier Calbet
Дата: 21 июля 2007
Перевод А.Тарасова, дата перевода: 2 августа 2007
При копировании материала обязательны указание автора, переводчика и ссылки на оригинал статьи и настоящую страницу как первоисточник перевода!
Вы можете быть профессиональным ученым или любителем, инженером или математиком, но если вам нужно быстро и легко производить численные расчеты и строить графики, тогда PDL (Perl Data Language) наверняка лучший из имеющихся свободных инструментов для этих целей. PDL столь же функционален, как и высокоуровневые проприетарные языки численных расчетов (например IDL или MATLAB). Система включает в себя все функции, которые вы хотите видеть в пакете для численных расчетов.
Введение
В этой статье я рассмотрю приложение численных методов в забавной области: мы нарисуем множество Мандельброта. Чтобы создать подобный фрактал, нужно произвести некоторые вычисления и затем нарисовать результат. Приведенные примеры просты, но их достаточно, чтобы ощутить использованный язык. Для данной задачи высокоуровневый язык численных расчетов - то, что нужно. Он предполагает быстрый цикл разработки из-за того, что язык высокоуровневый. Также с помощью этих инструментов легко рисовать высококачественные графики. И, как мы позже увидим, потеря производительности (относительно языков низкого уровня) при использовании этих систем невелика.Пример создания множества Мандельброта, рассмотренный в этой статье, будет проведен как в проприетарных, так и в свободных языках: PDL, IDL, MATLAB и Octave. Это позволит нам качественно сравнить их и занести в таблицу достоинства и недостатки каждого языка. Также будет проведено количественное сравнение, имеется в виду скорость вычислений. Для этих целей будет приведен код на языках C и FORTRAN.
Множество Мандельброта
В соответствии с Википедией, фрактал - это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Множество Мандельброта - классический пример фрактала. В этой статье я буду раскрашивать фракталы в немного другой артистичной манере (как на рисунке 1). Множество Мандельброта рождается из математического отношения между комплексными числами (см. Комплексные числа в Викиучебнике). Начиная с нулевого значения комплексной переменной (z), фрактал материализуется с помощью следующего соотношения:z = z * z + k,где k - комплексное число, остающееся постоянным в процессе вычисления. Конечное значение z существенно зависит от значения параметра k. Для некоторых значений k значение z сходится к некоторому конечному числу, а для других z расходится (неограниченно расходится). Чтобы избежать численных проблем с расходимостью, сделаем ограничение, чтобы значения z находились в пределах от -5 до 5 при каждой итерации. На рисунке фрактала оси X будет соответствовать действительной оси, а Y - мнимой. Обычно множество Мандельброта изображают так: точки расходимости рисуют одним цветом, точки сходимости - другим, таким образом граница между ними представляет собой множество Мандельброта. Я же буду использовать следующую формулу для цветов точек:
image = log (sqrt(Re(z) * Re(z) + Im(z) * Im(z)) + 1)где Re и Im обозначают соответственно действительную и мнимую части z. Итоговое изображение множества Мандельброта можно увидеть на рисунке 1.

Рисунок 1: Множество Мандельброта
PDL
PDL - это расширения языка Perl для численных расчетов и построения графиков. От Perl язык унаследовал чистый синтаксис хорошо устроенного языка. Вы также можете использовать богатый набор модулей из архива Perl (CPAN), чтобы включить в свою программу поддержку баз данных, обработку даты, взаимодействия между процессами, инструменты GUI и многое другое.Установка PDL
К сожалению, на большинстве популярных дистрибутивов GNU/Linux пакеты с PDL по умолчанию не установлены. Совсем плохо то, что для некоторых дистрибутивов пакетов PDL совсем нет или они некорректны. Если ваш дистрибутив GNU/Linux основан на Debian (как Ubuntu, Knoppix и т.д.), то вам повезло: у вас есть доступ к репозиториям Debian, и можно установить PDL безо всяких проблем. Для полноценной работы (а также для выполнения приведенного примера) нужно установить пакеты pdl, pgplot5 и pgperl. Как обычно вводите следующие команды (как root):# apt-get install pdl pgplot5 pgperlЕсли у вас не Debian, следуйте инструкциям в статье Installing PDL the quick and easy way.
Командная строка PDL
После установки PDL у вас появится возможность запустить его в командной строке. Для этого дайте в терминале командуperldl.
Система поприветствует вас примерно так:
xcalbet@debian:~$ perldl perlDL shell v1.33 PDL comes with ABSOLUTELY NO WARRANTY. For details, see the file 'COPYING' in the PDL distribution. This is free software and you are welcome to redistribute it under certain conditions, see the same file for details. ReadLines, NiceSlice, MultiLines enabled Reading PDL/default.perldlrc... Found docs database /usr/local/lib/perl/5.8.4/PDL/pdldoc.db Type 'help' for online help Type 'demo' for online demos Loaded PDL v2.4.2 perldl>Можно сразу попробовать функции PDL, введя команду
demo в приглашении PDL:
perldl> demoБудет приведен список демонстрационных скриптов, которые вы можете попробовать. Вам также стоит проверить библиотеку построения графиков PDL, чтобы убедиться, что она работает:
perldl> demo pgplotНа вашем экране должны появиться несколько графиков. Если этого не произошло, читайте Installing PDL the quick and easy way.
В следующем разделе я расскажу, как построить множество Мандельброта шаг за шагом с помощью командной строки PDL, чтобы вы смогли ознакомиться с основами PDL.
Множество Мандельброта с помощью PDL
Скалярные числа в Perl обычно обозначаются именем переменной с предшествующим знаком доллара. Такие переменные могут хранить лишь один объект, например, строку, более сложный объект, или, как в этом случае, численное значение.perldl> $npts=200; perldl> $niter=10;Только что мы задали
$npts - количество точек на стороне квадрата нашего будущего изображения и $niter - количество итераций для каждой точки. Теперь мы можем проверить содержимое этих переменных с помощью функции print:
perldl> print $npts; 200Базовые синтаксические единицы языка PDL - n-мерные массивы, которые обычно называют "вектор" ("piddle"). Вектор хранится в скалярной переменной Perl, как например действительная и мнимая часть z,
$zRe и $zIm:
perldl> $zRe=zeroes(double,$npts,$npts); perldl> $zIm=zeroes(double,$npts,$npts);Только что с помощью функции
zeroes мы создали двумерный квадратный массив нулей двойной точности. Его размер был указан ранее в переменной $npts.
Теперь вы можете создать матрицы, которые будут соответствовать значению константы k, используя функции xlinvals и ylinvals. Эти функции присваивают различные значения соответственно каждому столбцу или строке внутри определенного интервала.
perldl> $kRe=$zRe->xlinvals(-1.5,0.5); perldl> $kIm=$zIm->ylinvals(-1,1);Чтобы лучше понять, что делают
xlinvals и ylinvals, выведем подмножество матриц $kRe и $kIm с помощью метода slice:
perldl> print $kRe->slice('0:4,0:4');
[
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
]
perldl> print $kIm->slice('0:4,0:4');
[
[ -1 -1 -1 -1 -1]
[ -0.997998 -0.997998 -0.997998 -0.997998 -0.997998]
[ -0.995996 -0.995996 -0.995996 -0.995996 -0.995996]
[-0.99399399 -0.99399399 -0.99399399 -0.99399399 -0.99399399]
[-0.99199199 -0.99199199 -0.99199199 -0.99199199 -0.99199199]
]
Теперь мы можем начать цикл длиной в $niter итераций. Синтаксис циклов в Perl очень похож на синтаксис языка C:
perldl> for($j=0;$j<$niter;$j++){
Приглашение PDL изменится на:
..{ >
Это означает, что система поняла создание цикла, и ожидает, что рано или поздно будет его завершение.
Математические операции с векторами обычно выполняются поэлементно. Это происходит когда оба вектора имеют одинаковые размерности. Поэтому если вы умножаете или складываете несколько векторов одинакового размера, эти операции будут произведены поэлементно и результат будет получен в виде матрицы того же размера как и оригинальные матрицы. Можно использовать это свойство, чтобы произвести итерацию множества Мандельброта (z = z * z + k), которая, будучи разделенная на действительную и мнимую части, выглядит так (см. Комплексные числа в Викиучебнике):
..{ > $qRe=$zRe*$zRe-$zIm*$zIm+$kRe;
..{ > $qIm=2*$zRe*$zIm+$kIm;
Затем нужно применить трюк с ограничением значений между -5 и 5 после каждой итерации, в PDL это делается с помощью функции clip:
..{ > $zRe=$qRe->clip(-5,5);
..{ > $zIm=$qIm->clip(-5,5);
И наконец мы завершаем цикл:
..{ > }
На современном компьютере вычисления займут пару секунд. Когда вычисления завершатся, PDL снова отобразит приглашение командной строки.
Perl - модульный язык с возможностью по необходимости загружать другие модули. Чтобы иметь возможность строить графики, нужно загрузить два модуля:
perldl> use PDL::Graphics::PGPLOT::Window; perldl> use PDL::Graphics::LUT;Теперь можно открыть окно для построения графика:
perldl> $w=PDL::Graphics::PGPLOT::Window->new(Device=>'/xserve');Если на экране появилось пустое окно, значит, все идет нормально. Теперь можно выбрать цветовую палитру и вычислить конечное изображение:
perldl> $w->ctab( lut_data('rainbow2') );
perldl> $image=log( sqrt($zRe**2+$zIm**2) + 1);
Наконец, вы готовы нарисовать множество Мандельброта:
perldl> $w->imag($image);Должно появиться изображение, похожее на рисунок 1. Как вы только что убедились, численные расчеты в PDL просты и прямолинейны. Создание графиков функций и рядов данных также не проблема.
Все команды PDL, которые мы подробно описывали до этого момента, могут быть собраны в одной Perl-программе, назовем ее mandel.pl. Листинг программы приведен ниже:
#!/usr/bin/env perl
# Код PDL, изображающий множество Мандельброта
use PDL;
use PDL::Graphics::PGPLOT::Window;
use PDL::Graphics::LUT;
# Количество точек по стороне изображения и
# количество итераций в вычислении фрактального
# множества Мандельброта
$npts=1000;
$niter=51;
# Создание z = 0 (действительная и мнимая части)
$zRe=zeroes(double,$npts,$npts);
$zIm=zeroes(double,$npts,$npts);
# Создание константы k (действительная и мнимая)
$kRe=$zRe->xlinvals(-1.5,0.5);
$kIm=$zIm->ylinvals(-1,1);
# Итерации
print "Вычисление Mandel\n";
for($j=0;$j<$niter;$j++){
# Вычисление q = z*z + k в комплексной области
# q - временная переменная, хранящая результат
$qRe=$zRe*$zRe-$zIm*$zIm+$kRe;
$qIm=2*$zRe*$zIm+$kIm;
# Присваиваем z значения q, ограничивая в интервале
# от -5 до 5, чтобы предотвратить расходимость
$zRe=$qRe->clip(-5,5);
$zIm=$qIm->clip(-5,5);
}
# Строки, идущие далее, будут закомментированы при
# проведении сравнения производительности.
# Построение графика
print "Построение графика\n";
# Открываем окно для построения графика
$w=PDL::Graphics::PGPLOT::Window->new(Device=>'/xserve');
# Меняем цветовую палитру
$w->ctab( lut_data('rainbow2') );
# Создаем изображения
$image=log( sqrt($zRe**2+$zIm**2) + 1);
# Выводим изображение
$w->imag($image);
Углубляясь в множество Мандельброта
Можно детально рассмотреть любой участок множества Мандельброта, изменяя масштаб начальных значений k. Для этого изменяем команды инициализации k:# Создание константы k (действительная и мнимая) $kRe=$zRe->xlinvals(0.34,0.44); $kIm=$zIm->ylinvals(0.29,0.39);Результат показан на рисунке 2.

Рисунок 2: Приближаем множество Мандельброта
Подробнее о PDL
Разумеется, PDL намного богаче функциями, мы побывали лишь на вершине айсберга. Одна из функций, которая разительно отличает язык PDL от других языков - поведение математических операторов при операциях с матрицами, имеющими различные размерности. Эти свойства хорошо описаны в PDL indexing manual page и не будут рассмотрены здесь.
Другая важная функция - большой набор функций для манипуляций с размерами массивов и их содержимым. Вы уже знакомы с zeroes и xlinvals, но есть и другие функции, которые делают работу с массивами гораздо проще.
Существует множество замечательных учебных курсов по PDL. Некоторые приведены в списке в конце статьи.
Пришло время заняться состязанием.
IDL
IDL - проприетарный и определенно не свободный язык, нацеленный на численные расчеты. Он очень похож на PDL. Математические операторы в основном работают поэлементно, как и PDL. Хотя существуют и другие типы операций, например умножение матриц. Версия вычисления множества Мандельброта для IDL показана ниже. Надеюсь, комментарии будут понятны.
pro mandel
; Код IDL, изображающий множество Мандельброта
; Количество точек по стороне изображения и
; количество итераций в вычислении фрактального
; множества Мандельброта
npts=1000
niter=51
# Создание z = 0 (действительная и мнимая части)
zRe=dblarr(npts,npts)
zIm=dblarr(npts,npts)
# Создание константы k (действительная и мнимая)
a=dindgen(npts,npts)
kRe=a mod npts
kIm=float(floor(a/npts))
kRe=kRe*2.0/(npts-1.)-1.5
kIm=kIm*2.0/(npts-1.)-1
; Итерации
print,"Вычисление Mandel"
for j=1,niter do begin
; Вычисление q = z*z + k в комплексной области
; q - временная переменная, хранящая результат
qRe=zRe*zRe-zIm*zIm+kRe
qIm=2*zRe*zIm+kIm
; Присваиваем z значения q, ограничивая в интервале
; от -5 до 5, чтобы предотвратить расходимость
zRe = qRe < 5
zRe = zRe > (-5.)
zIm = qIm < 5
zIm = zIm > (-5.)
end
; Строки, идущие далее, будут закомментированы при
; проведении сравнения производительности.
; Построение графика
print,"Построение графика"
; Открываем окно для построения графика
device,decomposed=0,retain=2
Window,0,Xsize=400,Ysize=400
; Создаем изображения
image=alog( sqrt(Re^2+Im^2) + 1)
; Выводим изображение
tvscl,image
end
MATLAB
MATLAB - проприетарный язык, в основном направленный на математические расчеты. Он заточен под двумерные матрицы, но также эффективно работает с матрицами более высоких размерностей. Также этот язык, как будет видно позже, выполняется относительно медленно. Одно из преимуществ системы - имеется большой набор математических функций для разных задач, например, для решения обыкновенных дифференциальных уравнений, для задач минимизации и т.д. Ниже приведен листинг программы на MATLAB, изображающей множество Мандельброта, также с комментариями.
% Код MATLAB и Octave, изображающий множество Мандельброта
% Количество точек по стороне изображения и
% количество итераций в вычислении фрактального
% множества Мандельброта
npts=1000;
niter=51;
% Создание z = 0 (действительная и мнимая части)
zRe=zeros(npts,npts);
zIm=zeros(npts,npts);
% Создание константы k (действительная и мнимая)
kRe=repmat(linspace(-1.5,0.5,npts),npts,1);
kIm=repmat(linspace(-1,1,npts)',1,npts);
% Итерации
for j=1:niter
% Вычисление q = z*z + k в комплексной области
% q - временная переменная, хранящая результат
qRe=zRe.*zRe-zIm.*zIm+kRe;
qIm=2.*zRe.*zIm+kIm;
% Присваиваем z значения q, ограничивая в интервале
% от -5 до 5, чтобы предотвратить расходимость
zRe=qRe;
qgtfive= find(qRe > 5.);
zRe(qgtfive)=5.;
qltmfive=find(qRe<-5.);
zRe(qltmfive)=-5.;
zIm=qIm;
hgtfive=find(qIm>5.);
zIm(hgtfive)=5.;
hltmfive=find(qIm<-5.);
zIm(hltmfive)=-5.;
end
% Строки, идущие далее, будут закомментированы при
% проведении сравнения производительности.
% Построение графика
% Создаем изображения
ima=log( sqrt(zRe.*zRe+zIm.*zIm) + 1);
% Выводим изображение
imagesc(ima);
exit
Octave
Octave - свободный клон MATLAB. В сущности, главное достоинство данной системы - почти полное копирование функциональности MATLAB. Код, написанный для MATLAB, почти наверняка пойдет в Octave, может быть с небольшими изменениями. Поэтому программа для Octave, изображающая множество Мандельброта, выглядит в точности так же, как и для MATLAB. Будучи совершенным клоном MATLAB, Octave повторяет не только достоинства оригинала, но и недостатки, например, низкую скорость. Единственное исключение - цена и свободный доступ.C и FORTRAN77
C и FORTRAN77 являются никзоуровневыми языками, которые имеют длительный цикл разработки, однако программы на этих языках быстро выполняются. Они были включены в эту статью лишь с целью показать, насколько медленнее высокоуровневые языки по сравнению с этими более традиционными языками низкого уровня. Ниже приведен листинг на C.
#include <stdio.h>
#include <math.h>
// Количество точек по стороне изображения
#define NPTS 1000
int main(void) {
double zRe[NPTS][NPTS];
double zIm[NPTS][NPTS];
double kRe[NPTS][NPTS];
double kIm[NPTS][NPTS];
double qRe[NPTS][NPTS];
double qIm[NPTS][NPTS];
long int i,j,k,niter;
// Количество итераций в вычислении фрактального
// множества Мандельброта
niter=51;
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
// Создание z = 0 (действительная и мнимая части)
zRe[i][j]=0.;
zIm[i][j]=0.;
// Создание константы k (действительная и мнимая)
kRe[i][j]=(double)i*2.0/((double)NPTS-1.)-1.5;
kIm[i][j]=(double)j*2.0/((double)NPTS-1.)-1.;
}
}
// Итерации
//printf("Вычисление Mandel\n");
for(k=0;k<niter;k++){
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
// Вычисление q = z*z + k в комплексной области
// q - временная переменная, хранящая результат
qRe[i][j]=zRe[i][j]*zRe[i][j]-zIm[i][j]*zIm[i][j]+kRe[i][j];
qIm[i][j]=2.*zRe[i][j]*zIm[i][j]+kIm[i][j];
// Присваиваем z значения q, ограничивая в интервале
// от -5 до 5, чтобы предотвратить расходимость
zRe[i][j]=qRe[i][j];
zIm[i][j]=qIm[i][j];
if (zRe[i][j] < -5.) zRe[i][j]=-5.;
if (zRe[i][j] > 5.) zRe[i][j]=5.;
if (zIm[i][j] < -5.) zIm[i][j]=-5.;
if (zIm[i][j] > 5.) zIm[i][j]=5.;
}
}
}
// Строки, идущие далее, будут закомментированы при
// проведении сравнения производительности.
// Вывод изображения в стандартный вывод STDOUT
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
printf("%f ",log( sqrt(zRe[i][j]*zRe[i][j]+zIm[i][j]*zIm[i][j]) + 1.));
}
printf("\n");
}
}
Ниже листинг на FORTRAN:
program mandel
! Код FORTRAN77, изображающий множество Мандельброта
implicit none
integer npts
! Количество точек по стороне изображения
parameter (npts=1000)
real*8 zRe(npts,npts)
real*8 zIm(npts,npts)
real*8 kRe(npts,npts)
real*8 kIm(npts,npts)
real*8 qRe(npts,npts)
real*8 qIm(npts,npts)
integer i,j,k,niter
! количество итераций в вычислении фрактального
! множества Мандельброта
niter=51
do j=1,npts
do i=1,npts
! Создание z = 0 (действительная и мнимая части)
zRe(i,j)=0.
zIm(i,j)=0.
! Создание константы k (действительная и мнимая)
kRe(i,j)=dble(i)*2.0/(dble(npts)-1.)-1.5
kIm(i,j)=dble(j)*2.0/(dble(npts)-1.)-1.
enddo
enddo
! Итерации
! print *,"Вычисление Mandel"
do k=1,niter
do j=1,npts
do i=1,npts
! Вычисление q = z*z + k в комплексной области
! q - временная переменная, хранящая результат
qRe(i,j)=zRe(i,j)*zRe(i,j)-zIm(i,j)*zIm(i,j)+kRe(i,j);
qIm(i,j)=2.*zRe(i,j)*zIm(i,j)+kIm(i,j);
! Присваиваем z значения q, ограничивая в интервале
! от -5 до 5, чтобы предотвратить расходимость
zRe(i,j)=qRe(i,j);
zIm(i,j)=qIm(i,j);
if (zRe(i,j) < -5.) zRe(i,j)=-5.;
if (zRe(i,j) > 5.) zRe(i,j)=5.;
if (zIm(i,j) < -5.) zIm(i,j)=-5.;
if (zIm(i,j) > 5.) zIm(i,j)=5.;
enddo
enddo
enddo
! Строки, идущие далее, будут закомментированы при
! проведении сравнения производительности.
! Вывод изображения в стандартный вывод STDOUT
do i=1,npts
do j=1,npts
print *,log( sqrt(zRe(i,j)*zRe(i,j)+zIm(i,j)*zIm(i,j)) + 1.)
enddo
enddo
end program mandel
Таблица качественного сравнения
Таблица 1 качественно обобщает аспекты, упомянутые в предыдущих разделах.Пояснения к столбцам таблицы:
- Язык: название языка
- Версия: версия языка при тестировании
- Флаги: флаги компиляции или опции командной строки при тестировании
- Высокий уровень: является ли язык высокоуровневым, ориентированным на массивы, язык численных расчетов или нет
- Синтаксис: логичность синтаксиса языка и способность манипуляции массивами без привлечения циклов по индексам массива
- Функции: доступность математических функций и функции чтения/записи файлов научного формата
- Цена: бесплатно либо имеет высокую цену
| Язык | Версия | Флаги | Высокий уровень | Синтаксис | Функции | Цена |
| C | gcc 3.3.5 20050117 (pre-release) | -O3 | Нет | Плохо | Плохо | Бесплатно |
| FORTRAN77 | gcc version 3.3.5 20050117 (pre-release) | -O3 | Нет | Плохо | Плохо | Бесплатно |
| PDL | 2.4.1 | Нет | Да | Хорошо | Неплохо | Бесплатно |
| IDL | 6.2 linux x86 m32 | Нет | Да | Неплохо | Хорошо | Высокая |
| MATLAB | 7.1.0.183 (R14) Service Pack 3 | -nodisplay -nojvm | Да | Неплохо | Хорошо | Высокая |
| Octave | 2.1.64 (i686-Suse-Linux) | Нет | Да | Неплохо | Хорошо | Бесплатно |
Сравнение производительности
Сравнение производительности - хитрое дело. Это особенно имеет место для матричных языков, которые мы и рассматриваем.Явные циклы по индексам матрицы или if-конструкции не должны использоваться, так как они замедляют выполнение программы.
Многие функции этих языков являются высокоуровневыми, они решают задачи той или иной сложности. Выбор некоторых функций вместо других при одинаковом численном результате может существенно влиять на производительность. Простой пример - реализация эквивалента PDL-функции clip в системах MATLAB и Octave. В зависимости от выбранной реализации, язык получится быстрее или медленнее. В этой статье было выбрано решение, которое кажется более естественным для программистов MATLAB,
но этот прием, как видно из рисунка 3, дает некоторые преимущества системе MATLAB. Тогда как другое решение (не показано здесь) дает небольшое преимущество Octave. Другой пример - порядок циклов в языках C и FORTRAN. Если порядок циклов по индексам матрицы (i и j) поменять местами, производительность значительно уменьшается. В любом случае, это тестирование покажет порядок достигаемой производительности каждого языка.
В тестировании использовался персональный компьютер с процессором Intel Pentium 4 с тактовой частотой 2.8 ГГц, кэш 1024 Кб и 512 Мб памяти. Операционная система SuSE Linux 9.3 (i586) с версией ядра 2.6.11.4-21.15-2mp.
В этом тестировании я запускал программы, листинги которых приведены в статье, принимая во внимание следующее:
- Так как эти языки направлены на численные операции, было принято решение проводить сравнение на больших массивах. Для большей точности нужно большее число итераций. Поэтому, сравнение производительности проводилось со значениями $npts=2000 и $niter=1000. Это означает, что было вычислено изображение 2000 x 2000 точек с 1000 итераций на каждую точку.
- Подпрограммы отрисовки не были включены в тесты, была оставлена лишь численная часть. Как указано в комментариях к каждому листингу, последние строки кода, которые рисуют график, были закомментированы при сравнении производительности.
-
Для замера времени выполнения использовалась программа
time. Конечный результат, отображенный на рисунке 3 - сумма системного времени и времени пользователя. Чтобы сделать сравнения справедливыми, в случае C и FORTRAN время выполнения включало также и время компиляции кода. В любом случае, так как расчет 1000 итераций длится долго, для любого языка время компиляции или время запуска будет незначительным по сравнению с временем фактического вычисления. - Версии языков и флаги компиляции указаны в таблице 1.
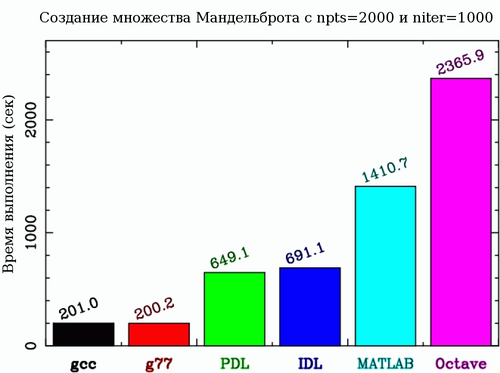
Рисунок 3: Показано время выполнения расчета множества Мандельброта.
Было установлено количество точек 2000 (что соответствует матрице 2000 x 2000)
и количество итераций 1000 (в текстах программ npts=2000 и niter=1000)
Заключение
Высокоуровневые матричные языки - полезный инструмент для разработки проектов с громоздкими численными вычислениями и построением научных графиков. С ними относительно легко быстро писать работающие расчетные программы. Это свойство было проиллюстрировано созданием множества Мандельброта.Было проведено качественное сравнение некоторых языков подобного рода (PDL, IDL, MATLAB и Octave), результаты в таблице 1. Не стоит говорить, что такое сравнение субъективно.
Сравнение производительности на примерах (см. рисунок 3) было проведено с целью показать, что некоторые высокоуровневые матричные языки, такие как IDL или PDL, способны показывать неплохую производительность, если избегать циклов по индексам массивов и if-ветвления. Такие языки лишь в 3 или 4 раза медленнее низкоуровневых языков, таких как C или FORTRAN77. MATLAB и Octave делают то же самое, но они явно медленнее IDL или PDL.
С моей точки зрения, PDL победил. Он предоставляет те же функции, что и дорогие проприетарные решения. В частности, математические функции и функции ввода/вывода являются почти полными эквивалентами функциям проприетарных программ, при этом в PDL работа с массивами производится быстрее. Если же принять в расчет и стоимость продукта, бесплатное (и свободное) против дорогого, то сравнение надо прекращать сразу. Используя PDL, вы никогда не получите сообщения типа "Нет лицензии для запуска программы", не упоминая даже о риске разработки программных проектов на основе языков, которыми владеют проприетарные компании.
