Библиотека сайта rus-linux.net
Статистический подход к проблеме спама
Оригинал: A Statistical Approach to the Spam ProblemАвтор(ы): Gary Robinson
Дата публикации: 1 Марта 2003
Перевод: Max Hvoshch
Дата перевода: 2013 г.
Использование байесовской статистики для определения спамовости электронных писем.
Ежедневно, большинство людей проводит значительное время отделяя спам от полезных писем. Думаю, не только мне одному кажется, что есть и более приятные дела. ПО для фильтрации спама может нам помочь.
Эта статья обсуждает одну из возможных математических основ ключевого аспекта спам фильтра - генерацию индикатора спамовости из коллекции токенов, представляющих содержание письма.
Подход, описанный здесь, поистине, является примером распределенной работы в лучших традициях открытого ПО. Пол Грэм (Paul Graham), автор книги по ЛИСП, предложил один из методов фильтрации спама в своей онлайн статье - План против спама (“A Plan for Spam”). Я воспользовался его подходом для генерации вероятностей связанных со словами, слегка изменив его, и применив, байесовские вычисления для работы с редко встречающимися словами. Далее, я предложил метод основанный на распределении хи-квадрата для объединения индивидуальных словесных вероятностей в комбинированную вероятность (точнее - пару вероятностей - смотрите ниже), представляющую электронное письмо. Наконец, Тим Питерс (Tim Peters) из Spambayes Project, предложил решение для создания весьма успешного индикатора спамовости, основанного на комбинированных вероятностях. На протяжение всего проекта, работа корректировалась постоянным тестированием конструкций с помощью, фильтра - Spambayes, написанного на питоне Тимом Питерсом, и фильтра - Bogofilter написанного на С Грегом Льюисом. Тестирование осуществлялось группой людей, участвующих в проекте.
Генерация вероятностей для слов
Предположим, что у нас есть группа писем (совокупность) для тренировки системы, и ПО, способное производить разбор каждого письма на составляющее слова. Далее, будем считать, что каждое письмо было вручную классифицировано, либо как не-спам (письмо, которое вы хотите прочитать), либо как спам (нежелательное письмо). Мы используем эти данные и ПО для обучения нашей системы, генерируя вероятность, представляющую спамовость, для каждого слова.
Для каждого слова, встречающегося в совокупности, мы рассчитываем:
- b(w) = (количество спам писем, содержащих слово w) / (общее количество спам писем).
- g(w) = (количество не-спам писем, содержащих слово w) / (общее количество не-спам писем).
- p(w) = b(w) / (b(w) + g(w))
p(w), грубо говоря, может быть интерпретирована как вероятность того, что случайно выбранное письмо, содержащие слово w, окажется спамом. Программы спам фильтрации могут рассчитать p(w) для каждого слова в письме, и использовать эту информацию, как основу для дальнейших расчетов, что бы определить, относится ли письмо к спаму или не-спаму.
Но, здесь есть одна очевидная проблема. В действительности, входной ящик конкретного человека может содержать и 10% и 90% спама. Естественно, это будет влиять на то, будет ли письмо с каким-то определенным словом отнесено к спаму или не-спаму.
Мы игнорируем это влияние в наших расчетах. Скорее это вычисление аппроксимирует вероятность того, что случайно выбранное письмо, содержащее w, оказалось бы спамом, в условиях, в которых половина писем относится к спаму, а другая половина к не-спаму. Достоинство этого подхода заключается в том, что классификация осуществляется независимо от относительной пропорции полученных спам и не-спам писем. Скорее, мы хотим, что бы классификация осуществлялась исключительно на основе наших характеристик. Такая методика довольно хорошо зарекомендовала себя на практике.
Обработка редких слов
При применении рассмотренного метода к редко встречающимся словам возникают проблемы. Например, если слово встречается в одном только письме, которое оказывается спамом, то p(w) равна 1.0. Очевидно, что далеко не факт, что все будущие письма, содержащие это слово, окажутся спамом. На самом деле у нас просто не хватает данных для определения правильной вероятности.
Байесовская статистика располагает действенными методами для работы с подобными ситуациями. Этот раздел статистики рассматривает вероятность через определение степени уверенности субъекта в истинности наблюдений.
В случае, если только одно письмо содержит определенное слово, и это письмо является спамом, степень нашей уверенности в том, что следующее письмо, содержащее это же слово, окажется спамом, не равна 100%. Это происходит из-за наличия нашей собственной исходной информации, которой мы руководствуемся. Из своего опыта мы знаем, что практически любое слово может появится как в спам, так и не в спам контексте, таким образом, одно или несколько частных значений не обеспечивают абсолютную уверенность в том, что вероятность правильна. Байесовский подход позволяет нам совместить нашу общую исходную информацию с полученными нами данными, что обеспечивает в должной мере учет обоих составляющих. Таким образом, мы определяем должную степень уверенности в том, будет ли увиденное вновь слово классифицировано как спам.
Эту степень уверенности f(w) мы определяем как:
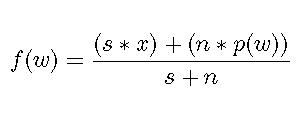
Уравнение 1
где:
- s - весомость, которую мы хотим присвоить нашей исходной информации
- x - наша предполагаемая вероятность, основанная на нашей исходной информации о слове, о котором у нас нет других данных или о слове, впервые попадающем в спам
- n - кол-во полученных писем, содержащих слово w
Это обеспечивает нам удобство при использовании x, для представления предполагаемой вероятности из исходных данных и s, как весомость, которую мы присваиваем этому допущению. На практике значения для s и x находятся через тестирование, что обеспечивает оптимизацию производительности. Разумные отправные точки 1 и 0.5 для s и x, соответственно.
Мы будем использовать f(w) вместо p(w) в наших расчетах. Это обеспечивает более реалистичные значения вероятностей, избавляя нас от экстремальных значений, которые зачастую возникают при недостатке данных. Эта формула прекрасно работает и в случае полного отсутствия данных, при котором f(w) является нашей предполагаемой вероятностью, основанной на исходных данных.
Те, кого интересуют детали того, как была выведена эта формула, читайте далее, а остальные могут перейти к следующему разделу.
Если вам уже знакомы принципы байесовской статистики, то у вас не должно возникнуть вопросов по выводу формулы. В противном случае, я бы порекомендовал разделы 1 и 2 из книги Дэвида Хекермана (David Heckerman) "Учебное пособие по байесовским сетям" ("A Tutorial on Learning with Bayesian Networks"), перед тем как продолжить.
Формула выше основана на предположении, что спам/не-спам классификация для писем, содержащих слово w, является биномиальной случайной величиной с априорным бета-распределением. Мы рассчитываем апостериорные ожидания после включения наблюдаемых данных. Мы проведем тест, эквивалентный эксперименту с многократным подбрасыванием монеты, для того чтобы определить, являются ли результаты непредвзятыми. Мы имеем: n - количество проб. В случае с монетой, каждое подкидывание монеты является пробой, и мы обычно считаем количество выпавших орлов. В нашем же случае пробой будет считаться анализ очередного письма из совокупности, содержащего слово "порно", с целью установления является ли это письмо спамом. Если да, то эксперимент будет считаться успешным. Очевидно, что этот эксперимент является биноминальным, так как возможные значения - да, или нет. Так же эти значения независимы, то есть факт наличия слова "порно" в одном письме, никак не связан с тем, окажется ли это слово в следующем письме. При проведении биномиального эксперимента с априорным бета-распределением, мы можем выразить ожидание того, что n+1 проба окажется успешной, с помощью уравнения 2.
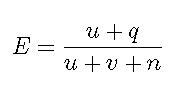
Уравнение 2.
- q количество успешных проб.
- n количество проб.
- u и v параметры бета- распределения.
Мы хотим показать, что уравнение 1 эквивалентно уравнению 2. Вначале, произведите следующую подстановку:
s = u + v s * x = u
Далее, замените q на n * p(w). Мы уже обсудили то, что p(w) это аппроксимация вероятности того, что случайно выбранное письмо со словом w является спамом в воображаемом мире, где спам и не-спам письма встречаются одинаково часто. Итак, n * p(w) аппроксимирует количество спам-писем, содержащих w, в условном мире. Это, в свою очередь, аппроксимирует количество успешных проб в нашем эксперименте, являясь, таким образом, эквивалентом q. На этом доказательство эквивалентности уравнения 1 и уравнения 2 закончено.
При тестировании замена p(w) на f(w) в расчетах, где, в противном случае, использовалось бы p(w), привело к более надежной классификации.
Комбинирование вероятностей
На этом этапе мы можем рассчитать вероятность f(w) для каждого слова, которое может появиться в новом письме. Основываясь на наших исходных данных, и данных нашей тестируемой совокупности, эта вероятность отражает нашу степень уверенности в том, что случайно выбранное письмо со словом w окажется спамом.
Таким образом, каждое письмо представлено набором вероятностей. Мы хотим объединить эти индивидуальные вероятности в совокупный индикатор спамовости или неспамовости для письма в целом.
В разделе статистики, известном как мета-анализ, пожалуй, наиболее распространенный способ объединения вероятностей принадлежит Р.Э. Фишеру (R. A. Fisher). Если у нас имеется набор вероятностей, p1, p2, ..., pn, то мы может поступить следующим образом. Вначале рассчитываем -2ln p1 * p2 * ... * pn. Далее, рассмотрим результат как распределение хи-квадрата с 2n степенями свободы, и используем хи-квадрат таблицу для вычисления вероятности получения результата, настолько же экстремального, или более экстремального, чем расчетный. Эта "объединенная" вероятность в полной мере включает в себя все индивидуальные вероятности.
Первоначальный набор вероятностей должен рассматриваться в рамках нулевой гипотезы. Например, если мы делаем предположение нулевой гипотезы относительно того, что результаты подбрасывания монеты не предвзяты, и далее, подбрасывая монету десять раз подряд, мы получаем только орлов, то в результате мы имеем вероятность (1/2)10 = 1/1024. В отношении к нулевой гипотезе такой экстремальный результат был бы маловероятен, если бы только монета ни была бы отклоненной. Следовательно, мы можем отвергнуть нулевую гипотезу и принять вместо нее альтернативную гипотезу, утверждающую, что результаты монеты предвзяты.
Мы можем использовать те же самые расчеты для объединения f(w). f(w) не являются реальными физическими вероятностями. Скорее они могут быть представлены как наши наилучшие попытки угадать эти вероятности. То же справедливо и для традиционного мета-анализа, с использованием вычислений Фишера. Вместо этого эти вероятности являются частью нулевой гипотезы.
Предположим, что наша нулевая гипотеза утверждает, что: "f(w) точна, и письмо является коллекцией слов, каждое из которых независимо от остальных, так что f(w) не находится в равномерном распределении". Теперь представим, что у нас есть слово "питон", для которого f(w) равна 0.01. Мы считаем, что это слово встречается в спаме только в 1% из всех случаев. Далее, с учетом сказанного выше, это маловероятное событие происходит, имея вероятность 0.01. Аналогично, каждое слово в письме имеет вероятность связанную с собой. Очень спамовые слова, такие как "порно", могут иметь вероятность 0.99 и выше.
Далее, используя вычисления Фишера, мы получаем вероятность для всего набора слов. Если письмо относится к не-спаму, то вероятно, что оно будет иметь ряд очень низких вероятностей, и относительно мало очень высоких вероятностей, в результате чего, комбинированная вероятность, рассчитанная по Фишеру, будет очень низка. Это позволит нам отвергнуть нулевую гипотезу и принять вместо нее альтернативную гипотезу о том, что письмо относится к категории не-спам.
Давайте обозначим эту объединенную вероятность как H:

Уравнение 3
где C-1() это обратная функция распределения хи-квадрата, используемая для получения значения p из случайной величины, распределенной по закону хи-квадрата.
Конечно, мы знаем с самого начала, что нулевая гипотеза не верна. Практически не существует писем, содержащих случайный набор слов, несмещенный в сторону не-спама или спама. Обычно письмо содержит достаточное количество слов того или иного типа. И, конечно, слова не являются независимыми по отношению друг к другу. Письма, содержащие слово"секс", более вероятно, будут содержать слово "порно", а письма, содержащие имя человека, программирующего на питоне, более вероятно будут содержать слово "питон". И f(w) не находится в равномерном распределении. Но, для целей определения спама, подобные отклонения от реальности обычно работают в нашу пользу. Они формируют неслучайный характер вероятностей, либо с высоким, либо с низким уровнем вероятностей, что помогает обеспечить статистический базис, необходимый для отвержения нулевой гипотезы в пользу альтернативных гипотез. Письмо либо является спамом, либо не-спамом.
При этом нулевая гипотеза, как правило, всегда отклоняется. Она используется лишь для того, что быть разрушенной одной из альтернативных гипотез.
Вероятно, здесь стоит упомянуть о ключевом различии между данным подходом и многими другими методами, предполагающими, что вероятности независимы. Например, это различие прослеживается в "байесовском цепном правиле", а так же в "наивной байесовской классификации". Эти два подхода также тестировались на большом количестве классифицированных человеком писем, но давали расхождения с человеческой оценкой чаще, чем рассмотренный выше метод.
Вычисления по этим методам технически не верны, так как требуют отсутствующей на самом деле независимости между частными значениями. Эта проблема не проявляется при использовании фишеровской методики, так как правильность расчетов не зависит от независимости данных. Фишеровский расчет структурирован таким образом, при котором нулевая гипотеза отвергается в пользу одной из альтернативных гипотез, интересующих нас. Каждая из этих альтернативных гипотез имеет зависимость, такую, как корреляция между словом "секс" и "порно", что создает экстремальные комбинированные вероятности.
Эти комбинированные вероятности являются вероятностями только исходя из предположения, что нулевая гипотеза практически наверняка окажется ложной. На самом деле комбинированная вероятность Фишера совершенно не является таковой, а скорее является абстрактным индикатором того, насколько мы должны склонятся к тому, чтобы принять нулевую гипотезу. Таким образом, в случае несостоятельности нулевой гипотезы, у нас не возникает вычислительных проблем. Наивный байесовский классификатор известен своей устойчивостью к искажениям, вызванным отсутствием независимости, но он не избегает их полностью.
Точно не известно, но одним из возможных факторов, определяющих высокую производительность фишеровского подхода в классификации спама, может быть отличающаяся реакция, при отсутствие независимости в данных.
Индивидуальные f(w) являются лишь аппроксимациями настоящих вероятностей (т.е. в случае, когда у нас очень мало данных о слове, наше предположение относительно спам вероятности, заданной f(w), может не отражать реальности). Но если мы посмотрим как вычисляется f(w), то мы увидим, что эта неопределенность уменьшается асимптотически, с приближением f(w) к 0 или 1, потому как такие экстремальные значения могут иметь только часто встречающиеся слова, которые почти всегда встречаются либо в спаме, либо в не-спаме. Наибольшее влияние на расчеты оказывают значения, близкие к 0. Для наглядности, рассмотрим влияние на произведение 0.01 * 5 при замене первого элемента на 0.001, и сравним это с влиянием на произведение 0.51 * 0.5, при замене первого элемента на 0.501. Не забываем, что метод Фишера основан на перемножении вероятностей. Таким образом, наша нулевая гипотеза нарушена тем фактом, что f(w)s не абсолютно надежна, что, тем не менее, имеет ничтожно малое значение для большинства слов при поиске доказательств спамовости: слова с f(w) близкой к 0.
В этом месте внимательные читатели зададутся вопросом. "Хорошо, я понимаю, что эти расчеты Фишера имеют смысл для неспамовых слов, имеющих вероятность, близкую к 0, но как насчет спамовых слов с вероятностью близкой к 1?" Хороший вопрос! Читайте дальше, чтобы узнать ответ, завершающий это обсуждение.
Индикатор неспамовости и спамовости
Вышеописанный расчет чувствителен к признакам неспамовости, особенно в случаях со словами, которые гораздо чаще появляются в не-спаме, чем в спаме. Это происходит из-за того, что вероятности, близкие к 0, оказывают значительное влияние на произведение вероятностей, имеющее центровое значение в расчетах Фишера. На самом деле, теорема 1971 года гласит, что фишеровский метод, при определенных обстоятельствах, является настолько же действенным, насколько это только возможно, при выявлении тенденций, лежащих в основе произведений вероятностей. (см. приложение).
Тем не менее, слова, ориентированные на спам, с f(w) близкой к 1, оказывают намного менее значительный эффект на вычисления. Можно считать, что это позитивное явление. В конце концов, для многих людей ошибочная классификация хорошего письма как спама окажется меньшей проблемой, чем ошибочная классификация спам письма как хорошего. Одно пропущенное спам письмо не нанесет серьезного урона, тогда как одно пропущенное хорошее письмо, не дошедшее до адресата, может оказаться проблемой. Таким образом, разумно иметь более чувствительную индикацию для неспамовых писем, и менее чувствительную индикацию для спама.
В реальном мире существуют решения, позволяющие существенно снизить процент ошибочно классифицированного спама, как не-спама, не повышающие при этом вероятность ошибочной классификации не-спама, как спама.
Ниже приведена наиболее эффективная методика, выявленная в недавних тестах.
Вначале поменяем на противоположные все значения вероятностей, путем вычитания их из 1 (т.е. для каждого слова, рассчитываем 1 - f(w)). Так как, f(w) представляет собой вероятность того, что случайно выбранное письмо из набора писем, содержащих w окажется спамом, то 1 - f(w) представляет вероятность того, что это же письмо окажется не-спамом.
Теперь произведем то же вычисление Фишера, что и ранее, но с (1 - f(w)), а не с f(w). Результатом окажется комбинированная вероятность, близкая к 0, отрицающая нулевую гипотезу, в случаях когда мы имеем дело с многочисленными спам словами. Назовем эту комбинированную вероятность S.
Теперь рассчитываем:

Уравнение 4
I - это индикатор, имеющий значения, близкие к 1, в случаях когда имеется превосходство доказательств, подтверждавших, что письмо является спамом, а значения, близкие к 0, говорят об обратном. Этот индикатор обладает парой интересных характеристик.
Предположим, что письмо имеет несколько очень спамовых слов, а так же несколько очень неспамовых слов. Ввиду того, что метод Фишера более чувствителен к значениям, близким к 0, и менее чувствителен к значениям, близким к 1, в результате может оказаться, что и S, и H, очень близки к 0. Например, S может иметь порядок 0.00001, а H может иметь порядок 0.000000001. На самом деле, подобные результаты, не так уж и редки в реальных письмах, как это может показаться. В одном из примеров, друг пересылает спам другому другу, в рамках переписки, посвященной спаму. В подобном случае найдутся явные признаки в пользу обоих заключений.
Во многих подходах, основанных например на байесовском цепном правиле, факт преобладания спамовых слов убедит классификатор в том, что письмо является спамом. Но, на самом деле, это не так очевидно, так как в примере с переправленным письмом мы имеем дело с не-спамом.
Весьма полезно, что I в таких случаях имеет значения близкие к 0.5, как и в тех случаях, когда мы не имеем достаточных доказательств в ту или иную сторону. В случаях, когда у нас имеется достаточно доказательств для обоих вариантов, I занимает предусмотрительную позицию. При реальном тестировании подобных писем, в отличие от черно-белого подхода большинства классификаторов, человек пришел бы к выводу, что подобные письма должны быть классифицированы как нечто среднее.
Spambayes Project, описанный в статье Ричи Хиндла (Richie Hindle) на странице 52, использует это, помечая письма с I близкой 0.5, как неопределенные. Это позволяет адресату письма уделить немного больше внимания письмам, которые невозможно классифицировать с достаточной степенью уверенности. Такая практика уменьшает шансы игнорирования письма адресатом из-за неправильной классификации.
Будущие направления
На сегодняшний день ПО, работающее по данной технологии, использует одно слово на один токен. Но возможны и другие подходы, такие как использование хэш-таблиц с фразами. Подразумевается, что математика, описанная здесь, может быть использована и в таких контекстах, и есть основания полагать, что системы, основанные на фразах, могут иметь более высокую производительность, хотя эта идея и противоречива. Статьи из Future Linux Journal скорее всего будут освещать разработки в этом направлении. CRM114 (см. приложение) являющаяся примером системы, основанной на использовании фраз, хорошо себя зарекомендовала, однако на момент написания этой статьи не прошла сравнительного тестирования на эталонных данных против других систем. (На момент написания этой статьи, CRM114 использует байесовское цепное правило для комбинации p(w).)
Заключение
Методы, описанные здесь, использовались в таких проектах как Spambayes и Bogofilter, и значительно улучшили производительность спам фильтрации. Будущие разработки, которые могут сочетать эти вычисления с методом, основанном на фразах, могут иметь еще более высокую производительность.
Реализация обратной функции распределение хи-квадрата на PythonПриложение
Вики, посвященная обсуждению вопросов по этой статье, а так же другим новостям и информации, относящийся к проблемам спама: www.wecanstopspam.org.
Обсуждение вопросов по этой статье: wecanstopspam.org/jsp/Wiki?GarySpamArticle.
Статья Пола Грэма - "План для Спама": www.paulgraham.com/spam.html.
Грэг Люис выполнил всесторонние испытания, описанной методики, и сравнил ее с другими методами: www.bgl.nu/~glouis/bogofilter.
Домашняя страница проекта Spambayes Project: spambayes.sourceforge.net/index.html.
Спам система, основанная на фразах, CRM114: crm114.sourceforge.net.
Теорема оптимальности Фишера 1971 года и ее описание взяты из следующего ресурсов: Little, R.; and Folks, J. (1971) “Asymptotic Optimality of Fisher's Method of Combining Independent Tests”. Journal of the American Statistical Association, 66, pp. 802-806.
Учебник по байесовским сетям Дэвида Хекермана: research.microsoft.com/scripts/pubs/view.asp?TR_ID=MSR-TR-95-06.






