ITK

Оригинал: ITK
Авторы: Luis Ibanez, Brad King
Перевод: А.Панин

Потоковая передача данных

Изначально тулкит ITK разрабатывался как набор инструментов для обработки изображений, полученных проектом Visible Human Project. В то время было совершенно ясно, что такой большой набор данных не сможет быть размещен в оперативной памяти компьютеров, которые обычно были доступны участникам сообщества исследователей медицинских изображений. Также данный набор данных все еще не может быть размещен в памяти стандартных настольных компьютеров, использующихся на сегодняшний день. Следовательно, одним из требований к разработке проекта Insight Toolkit было обеспечение возможности потоковой передачи данных изображения по конвейеру данных. Точнее, возможности обработки изображений больших размеров путем передачи блоков изображения через конвейер данных и последующей сборки результирующих блоков в конце конвейера.

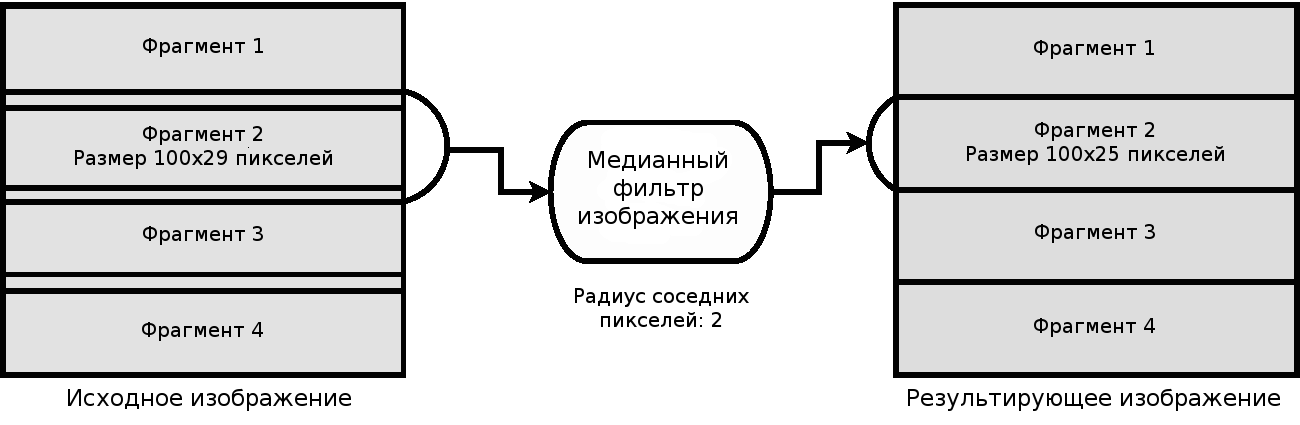
Рисунок 9.9: Иллюстрация процесса потоковой передачи изображения

Метод разделения области изображения проиллюстрирован на Рисунке 9.9 для конкретного примера медианного фильтра. Медианный фильтр вычисляет значение результирующего пикселя как статистическую медиану значений соседних пикселей исходного изображения. Размер границы из соседних пикселей является числовым параметром фильтра. В данном случае мы установили значение, равное 2 пикселям и это означает, что мы будем использовать соседние пиксели в радиусе 2 пикселей вокруг нашего результирующего пикселя. В результате нам необходим фрагмент изображения размером 5x5 пикселей с результирующим пикселем в центре и квадратной границей в 2 пикселя вокруг него. Обычно это называется Манхэттэн-радиусом (Manhattan radius). В тот момент, когда медианный фильтр получает запрос расчета значений пикселей запрашиваемого фрагмента выходного изображения, он обращается к предыдущему фильтру и просит его предоставить фрагмент большего, чем заданный с помощью спецификации запрашиваемого фрагмента размера, причем размер увеличивается на количество пикселей границы, в нашем случае на 2 пикселя. В специфическом случае, представленном на Рисунке 9.9, при запросе фрагмента 2 размером 100x25 пикселей, медианный фильтр передает запрос предыдущему фильтру, причем размер фрагмента устанавливается равным 100x29 пикселей. Вертикальный размер фрагмента, равный 29 пикселям, вычисляется как сумма 25 пикселей и размеров двух границ по 2 пикселя каждая. Следует отметить, что горизонтальный размер фрагмента не увеличивается в данном случае, так как этот размер является максимальным для рассматриваемого исходного изображения; следовательно, увеличенный размер, равный 104 пикселям (сумма 100 пикселей и размеров двух границ по 2 пикселя) уменьшен в соответствии с максимальным размером изображения, которое равно 100 пикселям по горизонтали.

Фильтры ITK, работающие с соседними пикселями, обрабатывают граничные условия одним из трех стандартных способов: устанавливают нулевое значение пикселей вне изображения, зеркально отражают значения пикселей по границе или повторяют значения граничных пикселей вне изображения. В случае медианного фильтра используется граничное условие Неймана нулевого потока (zero-flux Neumann boundary condition), которое просто означает, что значения пикселей вне границы фрагмента изображения устанавливаются равными значениям последних найденных пикселей в границах изображения.

Хорошо хранимым литературой по обработке изображений небольшим секретом является тот факт, что большинство сложностей реутилизации фильтров изображений относится к корректной обработке граничных условий. Это определенный симптом различий между теоретическими заданиями, которые встречаются во многих книгах, и практическим опытом разработки программного обеспечения для обработки изображений. В рамках проекта ITK эта задача была решена путем реализации набора классов итераторов изображения и соответствующего семейства классов для расчета граничных условий. Два этих семейства вспомогательных классов скрывают от фильтров изображений сложности управления граничными условиями в N-ном количестве плоскостей.

Процесс потоковой передачи данных изображения начинается вне фильтра, обычно с помощью классов ImageFileWriter или StreamingImageFilter. Два этих класса реализуют функции потоковой передачи данных, разделяя изображение на несколько фрагментов в соответствии с требованиями разработчика. После этого в ходе вызова их метода Update() они выполняют итерацию, запрашивая каждый из промежуточных фрагментов изображения. На этом этапе используются возможности API SetRequestRegion(), проиллюстрированного с помощью Рисунка 9.7. Этот вызов позволяет ограничить область расчета значений пикселей изображения с помощью фильтров фрагментом этого изображения.

median->SetInput( reader->GetOutput() );
median->SetNeighborhoodRadius( 2 );
writer->SetInput( median->GetOutput() );
writer->SetFileName( filename );
writer->SetNumberOfStreamDivisions( 4 );
writer->Update();

единственным новым элементом которого является вызов SetNumberOfStreamDivisions(), который устанавливает количество фрагментов, на которые будет разделено изображение для потоковой обработки с помощью конвейера. Для соответствия Рисунку 9.9 мы использовали значение, равное четырем и устанавливающее количество фрагментов для разделения изображения. Это значит, что объект writer выполнит запуск фильтра median четыре раза, причем каждый раз фильтру будет передаваться отличная структура запрашиваемого фрагмента.

Существуют интересные сходства между процессом потоковой обработки данных и процессом параллельной работы нескольких экземпляров заданного фильтра. В обоих случаях процесс основывается на возможности разделения задачи по обработке изображения путем разделения изображения на отдельные фрагменты, которые могут обрабатываться независимо. В случае потоковой обработки данных фрагменты изображения обрабатываются последовательно один за другим, а в случае параллельной обработки фрагменты изображения привязываются к отдельным потокам, которые в свою очередь привязываются к отдельным ядрам процессора. В конечном счете алгоритмический характер работы фильтров устанавливает то, возможно ли разделить результирующее изображение на фрагменты, которые будут обрабатываться отдельно на основании соответствующего набора фрагментов исходного изображения. В ITK функции потоковой и параллельной обработки практически ортогональны в том смысле, что существует API для управления процессом потоковой обработки существует отдельный API, предназначенный для поддержки реализации базовых функций параллельных вычислений с использованием множества потоков и фрагментов разделяемой памяти.

К счастью, с другой стороны, структура конвейера данных ITK поддерживает потоковую передачу данных для различных фильтров преобразований, используя тот факт, что все фильтры создают свое результирующее изображение и, следовательно, не перезаписывают область памяти, содержащую исходное изображение. Это приводит к затратам памяти, так как конвейеру приходится одновременно резервировать память и для исходных, и для результирующих изображений. Фильтры, осуществляющие такие операции, как переворот изображений, перестановка осей и геометрические изменения, попадают в эту категорию. В этих случаях конвейер данных управляет сопоставлением фрагментов исходного и результирующего изображений, требуя, чтобы каждый фильтр предоставлял метод с названием GenerateInputRequestedRegion(), который принимает в качестве аргумента прямоугольную область результирующего изображения. Этот метод производит расчет значений пикселей прямоугольного фрагмента исходного изображения, которые потребуются этому фильтру для расчета значений пикселей этого определенного прямоугольного фрагмента результирующего изображения. Этот постоянный обмен данными в рамках конвейера данных позволяет поставить в соответствие каждому блоку результирующего изображения соответствующий блок исходного изображения, который требуется для проведения расчета значений пикселей.

Если быть более точным, то можно сделать вывод о том, что ITK поддерживает поточную передачу данных изображения, но только при использовании "поточных" алгоритмов. Тем не менее, для того, чтобы быть прогрессивными в отношении оставшихся алгоритмов, мы должны трактовать это утверждение не как жалобу о том, что "невозможно реализовать поточную обработку данных при использовании этих алгоритмов", а как утверждение о том, что "наш стандартный подход к потоковой передаче данных не совместим с этими алгоритмами" на данный момент и мы надеемся, что в будущем сообщество изобретет новые техники для решения этой проблемы.

Продолжение статьи: Выученные уроки